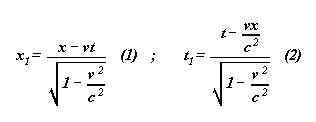
Through an original, purely mathematical and very elementary, study, I will demonstrate:

                    That Lorentz' formulas are interpretable in the classical space-time (euclidian space-time),
                    That they have very fundamental natural mechanical representations,
                    That these formulas do not exclude Galilean transformations ,
                    That speeds greater than c , c limit speed in Lorentz' formulas, are not excluded, by these
                                                                                                                                     transformations.
                    That the Einstein's principle of relativity is not the consequence of these transformations.
 
 

Beginning of the study
             As a simplification the formulas are studied here only in a one dimensional space .

             Let S an axis Ox , S₁ an axis O₁x₁
S₁ is parallel to S and S₁ slide along Ox at a constant speed, v ,
                       v verifying -c < v < c , c a given positive constant.
This means that the motion of O₁, origin of S_1, is determined in S, by the equation x = vt + x_{o .}
                        By an adequate choice of the origin O of S , we can always have x_o=0 .
Therefore we will take the equation x = vt  as equation of the motion of O₁ , relatively to S .

If E is an event of coordinates (x ,t ) in S , then the coordinates (x₁ ,t₁ ) of E in S₁ are,

by définition of Lorentz' transformations :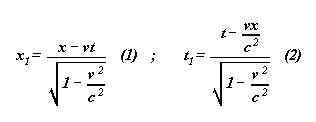 
 

Given the two systems S and S_{1 ,} one says that one passes from S to S₁ by the transformations of Lorentz of constant c .

                                   In the next, one puts: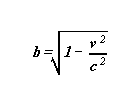
b is a constant dépendant only of v , b verifying :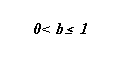( c being unchanged )
 

                                                                                                                      page 1
 

Another expression of t₁

From (1) we have : x = vt + bx₁ .
If we replace x by this expression in (2) , we obtain :
 
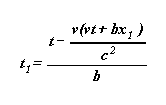Otherwise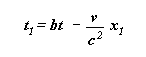 

this last formula brings out :

        1.  The slowing of clocks of S₁ , slowing proportional to the multiplicative factor b ,
        2.  The phasing-out of clocks of S₁ , phasing-out given by the additive term,
              term proportional to x₁ .
 
And more over, the formula x = vt + bx₁ ,compared to the Galilean's transformation
x = vt + x₁ , brings out the shortening of lengths of S₁ in the Ox direction, shortening always proportional to the multiplicative factor b .
 
In the following, I will represent systems S and S₁ , giving  c and v small numerical values that allow drawing very explicit figures.
These never seen figures will allow us to catch the full meaning of  Lorentz' transformations thoroughly.
 

Representation of S and S₁ in the particular case where :
 
 With these values one has   c² = 12 and b = 1/2 ,
 

that give for x₁ and t₁ : 

                Otherwise :
 
The unit of length in S is considered to be equal to 2 centimeters .
These various values enable convenient vizualizing of  S and S₁ systems at different times t of S . (See axis of figure 1)
The different drawings of the figure 1 are obtained in the following manner.

For drawing 1, one has  t=0 , and gives x all the values possible in the formulas :

                                               x₁ = 2x - 6t ; t₁ = 2t - 1/2 x .
With t = 0 , one has therefore : x₁ = 2x  and  t₁ = - 1/2 x

 For example, when  x = - 1 , one has : x₁ = -2 and t₁ = 1/2 .
 This mean that the point of S₁ in coincidence with the point of S of abscissa - 1 ,
(at the date t = 0 of S ) has for abscissa x₁ = -2 , and that the clock of S₁ that is found on this point,
indicates + 1/2  ( +1/2h to meaning that the number read is a time. h for hour) .
 
 

                                                                                                                    Page 2

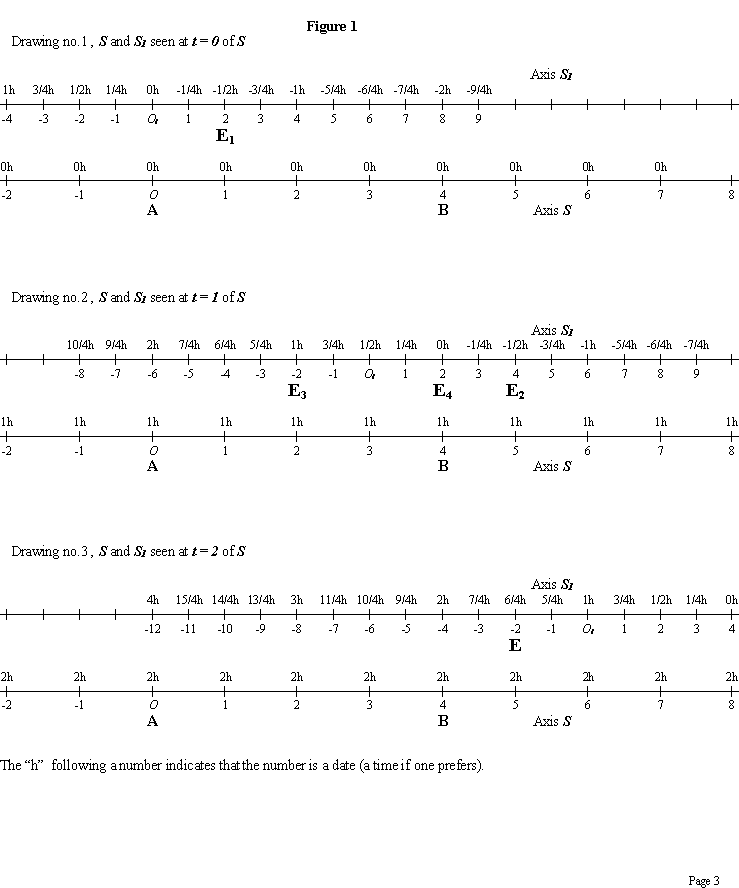
Similarly for all the other values of x, always with t = 0 , which gives the system
S₁ seen from S at the date t = 0 of S. (See drawing 1 of figure 1)

To obtain the second drawing, one takes t =1 , that gives x₁ = 2x - 6 and t₁ = 2 - 1/2 x , and one makes x
vary as previously, which gives the system S₁ seen from S at the date t = 1 of S .
 
One proceeds similarly to obtain drawing 3 by taking t = 2 (in S) , which gives
                                    x₁ = 2x - 12 and t₁ = 4 - 1/2 x .
In the drawings, the only times which are indicated are given by clocks placed on integer abscissas of systems.
 

The drawings of figure1 lead to the following remaks:

1. Units of length of S₁ (in the direction of the speed) are constant, and smaller than the units of length of S .
     In the drawings of figure1, the unit of S₁ (in the direction of the speed) is half that of S .

2. In S₁ , on each point, there is a clock, clock that is used to date events that happen in this point of S₁ .
    When in S₁ , an event happens in the point of abscissa x₁ of S₁ , the date in S₁ of this event is given by
    the clock of S₁ staying on x₁ , and by this one only. That is entirely comparable to terrestrial time zones.
    An event taking place in Paris is dated by the Paris time zone, and not by that of Moscow.
 
Example: On the first drawing (figure 1), E₁ represents any event (an explosion for example).

E₁ arise in S at the point of abscissa x = 1 , and the clock of S that is found at this point shows then
the date t = 0 . The coordinates of this event are in S : x = 1 and t = 0 .

This same event arise in S₁ at the point of abscissa x₁ = 2 , and at the date t₁ = - 1/2 , date gived by
the clock of S₁  placed at the point of abscissa x₁ = 2 of S₁ ( see, figure 1).

3. Simultaneous events in one system are no longer simultaneous in the other.

     Let me first define what are two simultaneous events in a system.

     Two events (two explosions, for example) are simultaneous for a system, if, and only if the dates given by
     the two clocks of the system that are found in the places (at the core) of these events, indicate the same
     numbers (the same time, the same date).
 
Example: The event E₁ of abscissa +2 in S₁ and of date - 1/2 always in S₁
         (an event indicated on the first drawing of figure 1), and the event E₂ of abscissa + 4 in S₁ and
         of date - 1/2 , always in S₁ (an event marked on the second drawing of figure 1) ,
         are simultaneous relatively to S₁ .

One notices that the coordinates of E₁ in S are x =1 and t = 0 , and that the coordinates of
E₂ in S are x = 5 and t = 1 . E₁ and E₂ are not simultaneous in S .

Similarly, two simultaneous events in S , not having the same abscissa, are not simultaneous in S ₁ .
Example:
On the drawing no. 2 of figure1, the event E₃ has for coordinates in S : x = 2 and t = 1 .
The event E₄ has for coordinates in S : x = 4 and t = 1 . E₃ and E₄ are therefore simultaneous in S .
The coordinates of E₃ in S₁ are: x₁ =   - 2 and t₁ = 1 .
The coordinates of E₄ in S₁ are: x₁ = 2 and t₁ = 0 .
E₃ and E₄ are not simultaneous in S₁ .
 

                                                                                                                     Page 4

4. The measure of the speed of a moving body, relatively to a moving system of reference,
     must refer to a more precise definition than commonly admitted, a definition that must
     exclusively  refer to clocks and abscissas (or coordinates) of the moving referential system.

Let me define therefore the speed of a moving body, relatively to a system of reference.
The definition is given in S₁ , but remain valid in any referential systems.

Let M be a point in translation on the S₁ axis. M passes on the point of abscissa x₁ of S₁ at the date t₁
(date given by the clock of S₁ staying on x₁ ).

Then M passes on the point of abscissa x'₁ of S₁ at the date t'₁ of S₁
( date given by the clock of S₁ that is put on x'₁ ).

The average speed of M , relatively to S₁ ,between points x₁ and x'₁ is : (x'₁ - x₁)/(t'₁ - t₁)

The limit of this average speed when x'₁ tends toward x₁ ( or when t'₁ tends toward t₁ ) gives the exact speed of M
at the point x₁ of S₁ at the date t₁ of S₁ ( t₁ given by the clock of S₁ that stays on x₁ ).

Example : Let us resume our drawings (see figure 2). Let M be a point in translation along axis S₁,
                therefore along axis S as well. By simplification, the speed of M , relatively to the motionless axis S ,
                is assumed to be constant.

                In the first drawing of figure 2, M is found on x₁ = 8 at the date t₁ = - 2 of S₁
                (date given by the clock of S₁ which is found on this point x₁ of S₁).

                In the second drawing of figure 2 , M is found on x'₁ = 0 at the date t' = 1/2
                (date given by the clock of S₁ which is found on this point x'₁ of S₁).

                The measured speed of M,  relatively to S₁ is :
                                                                   (x'₁ - x₁)/(t'₁ - t₁) = (0 - 8) /(1/2 - (-2) ) = - 3.2 .

                The measured speed of M,  relatively to S is : - 1 .
 

Remark : on the third drawing of figure 2, the coordinates of M , relatively to S₁ are
                                                       x"₁ = - 8 and  t"₁ = 3 .
We observe that (x"₁ - x'₁)/(t"₁ - t'₁) = (x'₁ - x₁)/(t'₁ - t₁) = (x"₁ - x₁)/(t"₁ - t₁) = - 3.2
This allows us to observe empirically that the speed of M , relatively to S₁ , is constant.

If M is moving, relatively to S , at the speed c (or -c) , one can observe experimentally on the drawings,
that the speed of M , relatively to S₁ , remains equal to c (or -c) , provided that to make measures as
in the previous case. I leave to the reader the care of this expériment.

I advise remaking drawings of the figures, taking c = 5 , v = 4 which gives b = 3/5 .
Drawings, as well as the representation of M moving at speed c , are simple with these values.
 

5. The measure of the length of a mobile segment, relatively to a system of reference (in movement)
    also has to refer to a far more rigorous definition than that given by intuition.

    This definition must refer exclusively to the abscissas(or coordinates) and the clocks of this system of reference.

    The definition is: let AB be a straight segment parallel to S₁ , a mobile or immobile segment relatively to S₁ .
    The origin A of AB passes at the point of abscissa x₁ of S₁ , while the clock of S₁ which is fixed at this point x₁
    of S₁ shows the date t₁ .
 

                                                                                                          Page 5

This number represents the difference of the abscissas, of the points of S₁ , from which one sees simultaneously,
relatively to S₁ , the extremities of the segment AB .
This definition is valid in all referential systems.
 

Example: let the segment AB , motionless relatively to S .

A of abscissa 0 in S , B of abscissa 4 in S (see figure 1).
On the first drawing of the figure 1, the origin A of AB is found at the point of abscissa x₁ = 0 of S₁ ,
and the clock of S₁ that is found on this point indicates the date t₁ = 0 .

On the second drawing of figure 1, the extremity B of AB is found on the point of abscissa x'₁ = 2
of S₁ , and the clock of S₁ that is found on this point, also indicates the date 0 .

Therefore, in S₁ , at " the instant " t₁ = 0 (of S₁ ) , the origin  A of AB is seen at  x₁ = 0 ,
and the extremity B is seen at  x'₁ = 2 . The algebraic measure of AB , relatively to S₁ , is therefore :
                                                    x'₁ - x₁ = 2 - 0 = 2 .

Therefore, the lenght of segment AB  is 2 in S₁ .
Any segment of length 4 ,taken on S , is seen under the length 2 in S₁ .

We can see immediately on the drawings of the figure 1 , that a segment of length 4 , taken on S₁
(and measured in S₁ ), has a length of  2 in S .
 
 
 
 
 

                                                                                                           Page 6

Mechanical systems that verify  Lorentz' transformations.

1. System built (arbitrary appearance) .

Let a motionless Ox axis in a classical space time. This axis is noted S .
Let an O₁x₁ axis noted S₁ , parallel to Ox , and in translation at speed v = 3  ,
relatively to Ox (in classical manner).

Axiomatically we take the unit of length  S₁ to be half  the unit of S , and, on each point of S₁
we place a clock , clocks that progress at the same speed twice as slow as those of S ,
and that are phased out, each one compared to the other, phasing out being -1/4 for a difference
of abscissa of 1 on S₁ .
And moreover, the clock that is placed on O₁ , the origin of S_{1 ,} indicates 0 at the date t = 0 of S .

More rapidly, on S₁ we measure, abscissas and times as indicated on the drawings of figure 1.
The manner to measure times in S₁ is in no way a surprise , just think of the terrestrial time zones.

The events taking place in Paris are dated by Parisian clocks, and those taking place in New York are dated
by the clocks of that town. When one says that an explosion happened at noon in New York ,
it is always implied that the hour is given by the clocks of that town. Similary in all other cities.

Let us return to our systems. Let E an event (an explosion, for example) that happens on the point of abscissa x of S ,
at the date t of S .
t is given by the clock of S that is found on the point of abscissa x of S , but has no importance because
S is a classical system whose all clocks are phased in.
 

The abscissa x₁ measured in S₁ of this event , as well as the date t₁ given by the clock of S₁ that is found
in the center of this event E (clock on the point of abscissa x₁ of S₁) when it happens ,
 

are given by :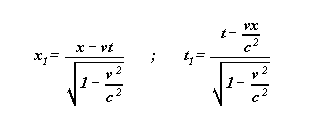
 

 With : 

One passes from S to S₁ by Lorentz' transformations, which one can experiment with different events
on the drawings of the figure 1, or the figure 2 .

 One notices that knowing x₁ and t₁ , one finds x and t with the two precedent formulas by replacing v by -v ,
therefore by the formulas :
 

                                                                                                      Page 8

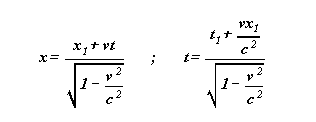
We pass from S₁ to S by Lorentz' formulas of same constant c .

Therefore we have two materially constructed systems, such that we pass from one to the
other by the Lorentz' transformations of same constant c .

The symmetry of these transformations does not in the least imply that S and S₁
are analogous from a material viewpoint. In our drawings, systems are totally dissimilar,
and by seeing them, no one would think that they are equivalent,
and nevertheless, one passes from one system to the other by the same transformations.

We will see later that these two systems are not at all equivalent in the description of some
phenomena, especially moving bodies in translation in S at speeds greater than c , lead to some
(pseudo) paradoxes in S₁ , entirely equivalent paradoxes to those obtained on the earth brought to
its time zones. A very fast plane that leaving Paris at noon (Parisian time) can arrive at eleven
o'clock in New York ( New York time) , and nobody would be shocked as one would be in relativity.

2° Natural system in classical mechanics.

One can wonder whether, in classical mechanics, there are systems that naturally obey
Lorentz' transformations, c being a constant attached to systems.

The reply is yes,they are, and it is even astonishing to see that they are very common.

Let a perfet elastic cord Ox , brought to an orthogonal referential Oxy system.

Any tranversal wave (of direction Oy ) on the cord is defined by two (any) functions f and g .

At any date t , the point of abscissa x of the cord has  y = f(ct -x) + g(ct + x)  for ordinate

c being a positive constant attached to the mechanical characteristics of the cord,
c is simply the speed of (transversal) waves along this cord.

y = f(ct -x) is on the cord, a wave propagating from left to right at  c speed,
y = g(ct + x) is on the cord, a wave propagating from right to left at the same speed c .
The sum of these two waves gives the state of the cord at any date t , and is the resultant wave.
The cord is oriented left to right.

Let t' and x' transformed of x and t by the Lorentz' formulas.
 
 

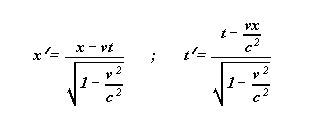
As previously ,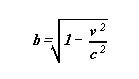
 

                                                                                                  Page 9

We find that :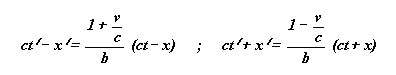
 

Let us put :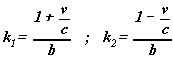 

k₁ and k₂ are two constants that do not depend either x or t , thus we find that

                          ct' - x' = k₁ ( ct - x ) and that ct' + x' = k₂ ( ct + x )

In the transversal perturbation y = f(ct -x) + g(ct + x) of the cord , replace x and t by x' and t' , we obtain :

                                 y = f(ct' -x') + g(ct' + x') = f(k₁ (ct -x)) + g(k₂ (ct + x))

Which gives a new perturbation (which is entirely possible) of the same vibrant cord.

This new perturbation is the old one, moving at v speed along the Ox axis.
It is what is shown in the program (relauk.exe) accompagnying this text.

One can observe that if M is a motionless point of the starting perturbation , this same point is in translation
at speed v along the Ox axis , in the pertubation put at speed v .

Example : the transversal perturbation of the cord, defined by :    y = f(ct -x) - f(ct + x)  ,
admits the point of abscissa x = 0 as a motionless point.

In the perturbation put at speed v :       y = f(ct' -x') - f(ct' + x') = f(k₁ (ct -x)) - f(k₂ (ct + x)) ,
the point of abscissa x = vt  always has for ordinate y = 0 , and is easy to verify.

"Permanent" points of the starting perturbation , are converted to "permanent" points at speed v in the
perturbation put at speed v .

We now wonder :
          What our clocks are on the cord ?
          And what  they become when the perturbation is put at speed v ? .

The same questions are asked about the units.

Here are the answers.
On each point of the cord , in a motionless system , times are simply given by a stationary periodical
referential wave (or perturbation), the unit of time being proportional to the vibratory period.

The unit of length is defined by the same referential wave, the chosen unit being proportional to the distance
of two consecutive "permanent" points .

In any system put at speed v along Ox , time and length references are given by the referential wave put at speed v
along Ox , in conformity with Lorentz' transformations , as indicated above.

Let us specify this with an example: it is the example displayed when one starts the attached program.
 

                                                                                                              Page 10

For a motionless system, we take as the stationary referential wave :

 
(One can take c = 5 to be in conformity with the animation of the program).

The points of abscissa x = k c , k relative integer , are the only permanent points of this referential wave.
The unit of measure is the distance divided by c , between two consecutive permanent points .

On each point of the motionless system is a clock , a clock that advances one unit each time the wave
crosses under its feet the Ox axis.
(The vibratory period of this wave is T = 2 , Ox axis is crossed by the cord at every unit of time.)

When we put the system in motion at v speed along the Ox axis, times and distances in the system in
motion are given by the referential wave put at v speed, thus by the wave:

(Constants k₁ and k₂ are defined above, in page 10.)

Each clock of the system in motion, always advances one unit each time the referential wave at speed v crosses
the Ox axis underneath. And the unit of length is obtained again by taking the distance between two consecutive
"permanent" points divided by c , always on the referential wave put at speed v.
The "permanent" points of the referential wave put at speed v , are in translation at speed v along Ox .

Now , "permanent" points are points of abscissas x = vt +bkc , k relative integer, b being defined above.
One sees that "permanent" points have drawn nearer according to multiplicative factor b .

A close observation of the animation of the attached program allows us to perfectly understand the above explanations.

This natural way of measure time and distance with the help of a referential wave, completely explains
Lorentz' transformations without exiting the framework of classical mechanics.

Complement : if Eo is the total energy , between two "permanent" points of the motionless "stationary wave" ,
the energy that takes into account the potential energy of the forces exerted by the wave on the extremities of the system
(forces exerted on the two permanent points), we find that the total energy Ev of the system at speed v is Ev = Eo/b
The démonstration is outside the limits of this elementary study.
The system behaves, relatively to the acceleration, as a mass of m = Ev / c^{2 .}

The results obtained on a vibrating cord are generalized to three dimensional elastic mediums.
 
 

Experimental study of moving bodies travelling in S at speeds greater than c .

The aim of this short study is to underline some paradoxes that prove that S and S₁ systems are not equivalent. S allows
to coherently describe the motion of a body moving at speeds greater than c , the description of the motion of this same
body becomes paradoxical (or incoherent) in S₁ .
 
 

                                                                                                                Page 11

Let us consider the drawings of figure 3.

Still with :

Let M be a moving body in translation at speed v = 3.5 , relatively to S , its time équation in S being x = 3.5 t

At t = 0 of S , M is on x = 0 of S , it is perceived in S₁ on the point of abscissa x₁ = 0 ,
and the clock of S₁ that is found on this point shows the date t₁ = 0.

At the date t' = 2 of S , M is on x' = 7 of S, it is then perceived in S₁ on the point of abscissa x'₁ = 2 ,
and the clock of S₁ that is found on this point shows the date t'₁ = 1/2 .

The speed of M measured in the referential S₁ is : (x'₁- x₁)/(t'₁ - t₁) = 2/0.5 = 4 .

The measure of the speed of M , relatively to S₁ , gives a value greater than that obtained in S , both speeds
beeing greater than c .This result seems opposed to common sense which suggests for the speed of M , relatively to S₁ ,
a smaller value than that obtained in S because M and S₁ are going in the same direction (same sense).

This paradox is simply due to the way of measuring times and distances in S₁ .
 

Now let N be another moving body in translation at speed 4 relatively to S
( the time equation of N in S being x = 4t ).
In S₁ , the clocks of S₁ that are found above N still show  0 , in other words, the moving body N crosses each clock
of S₁ when this clock shows the date 0 . ( see the figure 3)
N is therefore, relatively to S₁ , everywhere at the date 0 , the speed of  N , relatively to S₁ , is infinite .
S₁ is therefore a referential system in which it is impossible to descrbe the movement of N .
From this point of view , S and S₁ are not equivalent.
 

Now, let the body P  moving at speed v = 5 , relatively to S
(the time equation of P , relatively to S , being taken equal to : x = 5 t ).
At the date t = 0 of S , P is on O origin of S , the coordinates of P in S₁ are then
                                  x₁ = 0 and t₁ = 0 .
At t' = 1 of S this same moving body P is found on the point of abscissa x' = 5 (in S).
As previously, with the help of figure 3 , we find that the coordinates of P in S₁ are then
                                  x'₁ = 4 and t'₁ = -1/2 .

In S₁ , we have therefore : the starting date of P on O₁ , 0 h .
                                         the arrival date of P on x'₁ = 4 , -1/2 h .
In S₁ , the moving body P arrives 1/2 h before it has started.
Let us present this otherwise: in S₁ , a marksman shoots a bullet from O₁ at the date t₁ = 0 ,and at speed
v = 5 , speed relative to S .

This bullet arrives on x'₁ = 4 of S₁ at the date t'₁ = -1/2 h of S₁ . The bullet , according to the measurement of S₁ ,
arrives 1/2 h before it has started. In S₁ , for some phenomena, the effect precedes the cause, or seems to precede the cause.
This paradox is analogous to those created by terrestrial time zone gaps.

Once again , S₁ is inadequate for a coherent description of some phenomena. S and S₁ are not equivalent.

This fact therefore allows to determine which of S or S₁ is motionless.
The motionless system is that in which no paradox exists,  it is that in which the effect never precedes the cause.

It is always possible to add to S₁ a Galilean system S'₁ that follows S₁
( clocks and units of S'₁ are those of the classical mechanics , those of S ) .
In S'₁ , paradoxes disappear.

The simultaneous existence of different types of referential systems is not in the least contradictory.
A system of Lorentz (relativistic system) , can always be doubled by a Galilean system in which it is easier to reason.

                                                                                                      Page 13

The paradoxe of twins : this "paradox" is famous, I'll quickly mention it.

Let's take a system S₂ that coincides with S₁ (same as S₁). S₂ leaves S₁ , then rejoins S₁ by making the units coincide
(at the end of the experiment , the origin O₂ of S₂ is on O₁ origin of S₁ and the speed of S₂ is equal to the speed of S₁ ).

We notice then that the clocks of S₂ are late compared with those of S₁ , and this whatever the intermediate
accelerations of S_{2 ,} S₁ continuing its uniform translation.
In the attachedprogram, the T key allows this experiment.
We can also draw different pictures as those of figures 1,2,3 with three systems to visualize this paradox.
This paradox is explained by Lorentz' formulas, without the help of any other theory.
 

                                            Cabala Serge . 1975 , 1976, 1977 , 1980 , .... ,1999 , january 2000
 

P.S.

My mains works on this subject are:
- This study.
- Relativity by Waving Strings. (1975-76) classified in Archives Originales du CNRS (France) from 1977 (183 pages)
- Relativity by Elastic Mediums (1981, 185 pages)
- The Changes of variables that convert all functions of d'Alembertian equal to zero into functions of same property ,
                                                                              with extension to Klein-Gordon equations (1988, 129 pages)

All these works have been accepted , and an ex-director of the French CNRS had underlined its quality.
They are neither taught not published on a large scale in order to preserve the traditional relativity.

It is to be regretted to see that science has been transformed into religion , by maintaining some unnecessary
and constraining dogmas , such as the principle of relativity and its limit speed.
The formulas of relativity being only classical mechanics formulas of elastic mediums, it is
unnecessary to wish to establish them from new principles, that arbitrarily limit their applications,
and introduce a degree of strange thought .

When one speaks about relativity, one always quotes the Michelson and Morley experiments,
done in 1881 and 1887 , on the detection of the wind of ether relative to the earth.

Let us reflect a bit, after having read what precedes and use the program on waves.
If electromagnetic fields are only particular "waves" of the ether considered as an elastic medium,
the only manner to put these "waves", or electromagnetic fields, in translation, is to use Lorentz' formulas,
and this in the framework of classical mechanics.
Atoms of matter are held together by "stationary" electromagnetics fields .
The setting in uniform lengthwise motion of a ruler of any material, puts the "stationary waves"
in motion , these "waves" are contracted in the direction of the motion and are phased out (see the program) ,
the ruler's atoms are compacted and the ruler is shortened.
The wind of ether becomes thus undetectable by this experiment.

The explanation of the negative result of this experiment, by the contraction of bodies in motion,
had already been given by Fitzgeral (1893), but the actual atomic constitution of the matter, not being known
(the atomistic constitution of the matter being even hardly denied by famous scientists) ,
this mechanical explanation seemed very difficult to admit.
One could not conceive, that materials of very different hardness at same velocity, can be contracted
in the same way.

The Michelson and Morley experiment , finely analyzed is in favor of the ether.
 

                                                                                                      Page 14

For these detractors: if the moon exerts an attraction on the earth , a sea swell must exist
in front of the moon and a hollow at the antipodes side.
But there are always two sea swells, one in front of the moon and another to lunar antipodes,
there is therefore no attraction.

The phenomenon of tides roughly explained by the universal attraction is opposite to reality,
but the universal attraction finely used with acceleration (what I do not do here) explains
perfectly why there are two swells.

It is similary with the Michelson and Morley experiment : roughly analized, it is in disfavor of the ether,
finely analized, it becomes one of the proofs.
 

                         I hope I have communicated the pleasure of at last a true Cartesian relativity.

                                                                                                              Page 15