Ondes et Relativité
Serge Cabala
Aspects historiques des ondes
et de la relativité.
Cliquer sur "Home
page" pour obtenir la page principale.
Chapitre V
Période 1887-1905
Paragraphe 7.
Découverte expérimentale des masses variables;
formules d'Abraham, de Lorentz, d'Einstein.
L'utilisation du tube de Crookes ne s'arrête
pas à la découverte des électrons. On multiplie les
expériences en utilisant des tensions de plus en plus grandes et
de 1897 à 1904 il va fournir des résultats étonnants
.
Les mesures de la déviation des rayons cathodiques
par des champs magnétiques et électriques calibrés
(de forme et d'intensité donné), permettent de calculer la
vitesse de l'électron, et le rapport e/m de sa charge à sa
masse. On trouve toujours le même rapport tant que la tension d'alimentation
du tube n'est pas trop élevée (quelques milliers de volts).
Mais lorsqu'elle augmente considérablement, jusqu'à plusieurs
centaines de milliers de volts avec les grosses bobines de Ruhmkorff de
l'époque, on constate que le rapport e/m diminue, et que la vitesse
constatée est inférieure à la vitesse théorique
calculée avec un rapport e/m constant.
Pour une tension de 200 000 volts, la vitesse théorique
est de 265 000 km/s, la vitesse réelle est de 208 000 km/s. Et pour
un tension de 300 000 volts, on a un vitesse théorique de 325 000
km/s (supérieure à celle de la lumière) mais la vitesse
réelle est seulement de 233 000 km/s.
Les rayons bêta, découverts en 1899,
produits par du radium par exemple, ont un comportement identique aux rayons
cathodiques. On en déduisit qu'ils étaient constitués
d'électrons (les atomistes bien-sur, car les anti-atomistes sont
opposés à tout ce qui est corpusculaire). En les déviant
par des champs électriques et magnétiques, on calcule leur
vitesse et le rapport e/m. Les constatations furent encore plus nettes
qu'avec les rayons cathodiques. Certains rayons bêta atteignent plus
de 90% de la vitesse de la lumière, et le rapport e/m devient très
inférieur à celui obtenu pour les petites vitesses. En les
ralentissant (on les fait passer à travers une fine paroi d'aluminium
par exemple) on obtient des vitesses et des rapports e/m égaux à
ce qui est obtenu dans un tube de Crookes sous tension faible.
Dès 1901 Kaufmann avait noté que le
rapport de la charge à la masse d'un électron diminuait considérablement
lorsque sa vitesse s'approchait de celle de la lumière.
On décida que seule la masse augmentait avec
la vitesse, et que la charge restait invariable.
Les expériences montrèrent de plus,
que pour une particule donnée, la masse longitudinale était
plus grande que la masse transversale. (Lorsque la vitesse augmente, la
force nécessaire, pour accroître le module de sa vitesse,
augmente plus vite que celle qui sert à la dévier.)
Max Abraham donna dès 1903 les première
formules pour ces inerties, puis Lorentz en donna d'autres en 1904, qui
se révélèrent être les bonnes après de
multiples expériences.
Les expériences faites exprès en 1906,
avec beaucoup de précautions, par Kaufmann, pour vérifier
les formules de Lorentz, semblaient confirmer celles d'Abraham et non celles
de Lorentz.
Ce n'est qu'en 1908 que Bucherer monta des expériences
encore plus rigoureuses qui permirent de montrer que les masses longitudinales
et transversales obéissent aux lois données par Lorentz.
D'autres expériences faites en 1910 par E.
Hupka, en 1913 par Cl. Schaefer et G. Neumann, en 1915 par Ch. E. Guye
et Ch. Lavanchy, confirmèrent toujours les formules données
par Lorentz.
Pour Lorentz, la masse longitudinale est :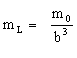 ,
la transversale est :
,
la transversale est :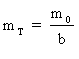 ,
,
avec 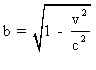 .
v: vitesse de la particule, c: vitesse de la lumière. mo
étant la masse au repos (ou aux faibles vitesses). mo
, pour un électron, sera précisé plus bas.
.
v: vitesse de la particule, c: vitesse de la lumière. mo
étant la masse au repos (ou aux faibles vitesses). mo
, pour un électron, sera précisé plus bas.
Ces deux formules de masse longitudinale et transversale
se résument en une seule sous la forme F = d(mv)/dt
, F et v désignant le vecteur force et le vecteur
vitesse, avec m = mo/b .
Les formules d'Abraham sont plus compliquées, les voici:
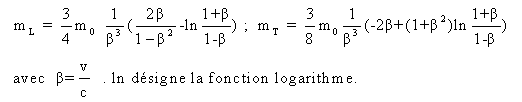
Les formules de Lorentz et d'Abraham sont assez
voisines contrairement aux apparences.
Pour v voisin de zéro, on trouve mL
= mT = mo avec les deux séries de formules.
Les formules d'inerties données en juin 1905
par Einstein, dans sa célèbre publication, sont :
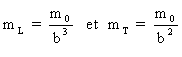 . On constate que la masse
transversale mT donnée par Einstein, diffère de
celle donnée par Lorentz en 1904. La bonne formule est celle de
Lorentz. Einstein a comparé l'accélération observée
dans le système au repos, avec la force calculée dans le
système en mouvement, d'où la différence. Cette erreur
prouve la difficulté de raisonner en relativiste pur.
. On constate que la masse
transversale mT donnée par Einstein, diffère de
celle donnée par Lorentz en 1904. La bonne formule est celle de
Lorentz. Einstein a comparé l'accélération observée
dans le système au repos, avec la force calculée dans le
système en mouvement, d'où la différence. Cette erreur
prouve la difficulté de raisonner en relativiste pur.
Abraham considère que l'électron conserve
toujours une forme sphérique, alors que pour Lorentz, l'électron
s'aplatit selon le facteur b dans le sens de la vitesse. C'est ce qui explique
la différence de formules.
Paul Langevin, considérant que l'électron
s'aplatit en conservant son volume, trouva encore d'autres formules pour
les masses.
En confrontant les formules d'Abraham à l'expérience,
Kaufmann conclut que l'électron "n'est autre
chose qu'une charge électrique, distribuée sous un volume
ou une surface de dimensions très petites". Au vu de ce résultat
expérimental, Abraham et Lorentz admettent pour l'électron,
l'hypothèse d'une masse inerte d'origine totalement électromagnétique.
Je laisse Poincaré exprimer la chose autrement
: "Les calculs d'Abraham nous font connaître
la loi suivant laquelle la masse fictive varie en fonction de la
vitesse; l'expérience de Kaufmann nous fait connaître la loi
de variation de la masse totale. La comparaison de ces deux lois
nous permettra donc de déterminer le rapport de la masse réelle
à la masse totale. Telle est la méthode dont s'est servi
Kaufmann pour déterminer ce rapport. Le résultat est bien
surprenant : la masse réelle est nulle."
m0 désigne donc, dans toutes les
formules précédentes, pour un électron immobile, son
inertie électromagnétique, sa masse fictive, celle
dont parle Poincaré.
Une sphère électriquement chargée
présente vis à vis de l'accélération une inertie
plus grande que si elle était non chargée. Ce supplément
d'inertie est proportionnel au carré de la charge, et est inversement
proportionnel au rayon de la sphère.
Pour les faibles vitesses, cette inertie supplémentaire
est : 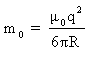 . m0
est appelé masse électromagnétique de la sphère.
R est le rayon de la sphère, q sa charge électrique,
. m0
est appelé masse électromagnétique de la sphère.
R est le rayon de la sphère, q sa charge électrique,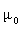 la
perméabilité magnétique du vide (
la
perméabilité magnétique du vide (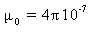 ).
).
Les unités employées sont les unité
M.K.S. actuelles.
C'est cette valeur de m0 qui intervient
dans les formules des masses variables données ci-dessus par Lorentz
et Abraham, et les expériences ne semblent pas indiquer l'existence
d'une autre masse. (La formule de m0 fut donnée la première
fois par Abraham.)
En supposant qu'un électron isolé
au repos est une sphère électriquement chargée, dont
la masse inerte n'est que purement électromagnétique, on
trouve que son rayon est : 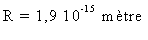 .
.
Il est à signaler qu'en 1881, J.J. Thomson
dans sa publication "On the electric and magnetic
effects produced by the motion of electrified bodies" introduit
déjà la notion de masse électromagnétique longitudinale.
Mais ses résultats diffèrent de ceux donnés par Lorentz
ou Abraham.
Suite du texte.
Sommaire.
Home
page
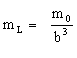 ,
la transversale est :
,
la transversale est :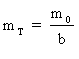 ,
,
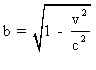 .
v: vitesse de la particule, c: vitesse de la lumière. mo
étant la masse au repos (ou aux faibles vitesses). mo
, pour un électron, sera précisé plus bas.
.
v: vitesse de la particule, c: vitesse de la lumière. mo
étant la masse au repos (ou aux faibles vitesses). mo
, pour un électron, sera précisé plus bas.
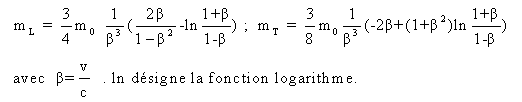
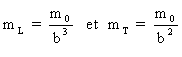 . On constate que la masse
transversale mT donnée par Einstein, diffère de
celle donnée par Lorentz en 1904. La bonne formule est celle de
Lorentz. Einstein a comparé l'accélération observée
dans le système au repos, avec la force calculée dans le
système en mouvement, d'où la différence. Cette erreur
prouve la difficulté de raisonner en relativiste pur.
. On constate que la masse
transversale mT donnée par Einstein, diffère de
celle donnée par Lorentz en 1904. La bonne formule est celle de
Lorentz. Einstein a comparé l'accélération observée
dans le système au repos, avec la force calculée dans le
système en mouvement, d'où la différence. Cette erreur
prouve la difficulté de raisonner en relativiste pur.
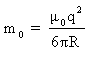 . m0
est appelé masse électromagnétique de la sphère.
R est le rayon de la sphère, q sa charge électrique,
. m0
est appelé masse électromagnétique de la sphère.
R est le rayon de la sphère, q sa charge électrique, la
perméabilité magnétique du vide (
la
perméabilité magnétique du vide (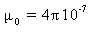 ).
).
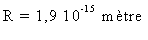 .
.