On a : (1)
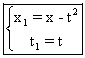 ; (2)
; (2)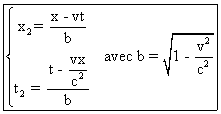
1° Exprimons (xi, ti)
en fonction de (x, t).
On a : (1)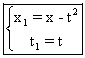 ; (2)
; (2)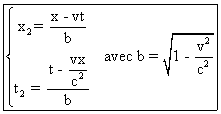
On a : (3) 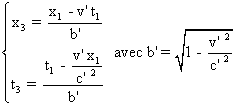 , par définition
des systèmes.
, par définition
des systèmes.
Ce qui donne : (4) 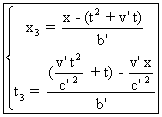
L'expression (4) s'obtient en remplaçant dans (3) (x1,
t1) par l'expression en fonction de (x,
t) donnée dans (1).
Exprimons maintenant (x3, t3) en fonction de (x2, t2).
On a : 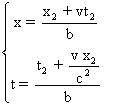 On remplace x et t par
ces dernières expressions dans (4).
On remplace x et t par
ces dernières expressions dans (4).
On obtient : (5)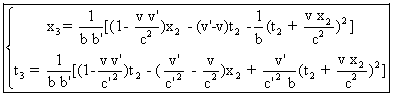
Complément: exprimons
(x, t) en fonction de (x3, t3)
.
On trouve : (6)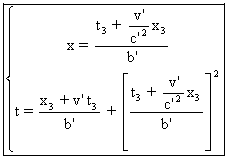
Ces
dernières formules s'obtiennent soit à partir de (4), soit
directement en passant de S3 à
S1, puis de S1
à S.
On constate ainsi que les transformations (4) réalisent une bijection
de R2 sur R2 . R désignant
l'ensemble des nombres réels.
2° L'équations du mouvement de M dans S
est x = kt .
En remplaçant x par kt dans (4), on obtient
: (7) 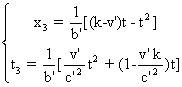 On trouve :
On trouve : 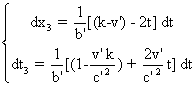
La vitesse de M par rapport à S3
est donc : (8)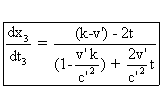
Cette vitesse est donnée en fonction de t.
Si v'=0, dx3/dt3
= k-2t. On suppose désormais que v' est non nul.
Les variations de dx3/dt3 en fonction de t sont résumées dans le tableau suivant.
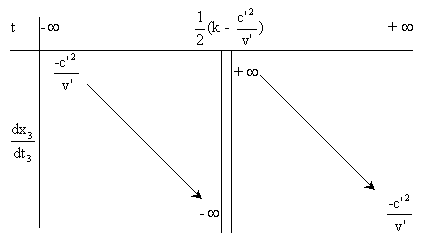
Ce qui répond à la discussion demandée dans cette deuxième question.
3° a) Dans S, l'équation du mouvement
de l'extrémité de la règle est : x = kt' +L .
En remplaçant
x par kt' + L, dans (4), on obtient: (9)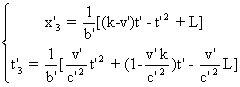
Ici t est remplacé
par t' , et (x3, t3)
est remplacé par (x'3, t'3)
pour bien distinguer l'origine de l'extrémité de la règle.
t et t' ne sont
pas obligatoirement égaux, lorsque l'on considère les formules
(7) et (9) à la fois.
t' et t désignent
le temps dans S.
Le mouvement
de l'origine de la règle est décrit dans S3
par (7), celui de l'extrémité par (9).
Pour t'= t donné
on constate que :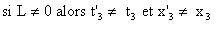 .
.
L est une constante
indépendante de t'.
On trouve comme dans la
seconde question,
que la vitesse de l'extrémité
de la règle est : (10) 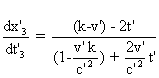 .
.
Pour t'= t donné,
la vitesse de l'origine est la même que celle de l'extrémité,
dans S3.
Mais attention, la
formule (8) donne la vitesse de l'origine de la règle à une
date t3 de S3
,
alors que la formule
(10) donne la vitesse de l'extrémité de la règle à
une date t'3 de S3
différente de t3 .
Nous allons comparer les vitesses dans S3, de l'origine et de l'extrémité de la règle lorsque t'3=t3.
Notons Or
líorigine de la règle, Er son extrémité.
Le mouvement
de Or est donné dans S3
par les équations (7) 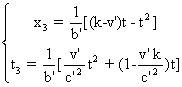
Soit t3
donné, déterminons toutes les dates t de S pour lesquelles
on obtient ce t3 dans les équations
(7) du mouvement de Or.
On suppose dans
tout ce qui suit que ví est non nul . ví=0 rend les repères S1
et S3 identiques.
Líéquation
à résoudre est : 
Le discriminant
de cette dernière équation est : 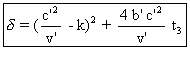
Posons : 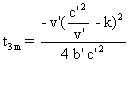 . Si
. Si 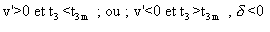 , líéquation nía
pas de solution.
, líéquation nía
pas de solution.
Aucune valeur de t
ne donnera t3 . Plus précisément,
jamais aucune horloge de S3 ne marquera
t3 lorsque Or passera dessus.
On suppose désormais
que 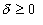 .
.
Nous obtenons deux
valeurs possibles pour t ,
valeurs qui sont : 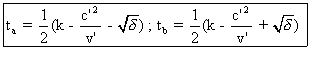 On remarque que :
On remarque que : 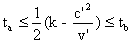
A la date t3
de S3 , Or est :
Soit en 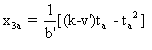 ,
et sa vitesse dans S3 est alors
,
et sa vitesse dans S3 est alors 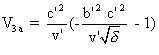
Soit en 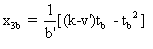 ,
et sa vitesse dans S3 est alors
,
et sa vitesse dans S3 est alors 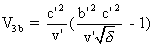
Je rappelle que : 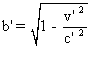 .
.
Les vitesses
V3 a et V3 b
síobtiennent en remplaçant dans líexpression (8) , t par t
a puis par tb .
On remarque
que ces deux vitesses sont différentes.
On remarque de
plus que si 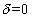 , ces vitesses deviennent
infinies, ce que líon peut voir dans le tableau de la seconde question.
, ces vitesses deviennent
infinies, ce que líon peut voir dans le tableau de la seconde question.
Le mouvement
de Er est donné par les équations (9)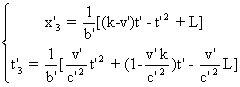
t3 étant donné, trouvons toutes les valeurs de tí qui donnent par les formules (9) tí3= t3 .
De
façons analogue à ce qui a été fait pour Or
,
on trouve que tí est solution de líéquation : 
Le
discriminant de cette équation est : 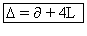 .
.
On
suppose dans ce qui suit que  .
.
On
trouve deux valeurs pour tí qui sont : 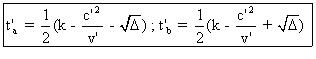
Lorsque
L tend vers zéro, tí doit tendre vers t .
Pour t3 donné, si líon considère
Or à la date ta dans S,
Er doit être considéré à la date tía
dans S pour pouvoir les considérer simultanément dans
S3.
De même pour tb et tíb
.
En
définitive, à la date t3
de S3 , on a :
Soit Or est en 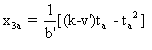 et Er
est en
et Er
est en 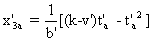
Les vitesses respectives de Or et Er sont alors : 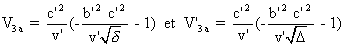
Soit
Or est en 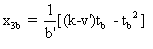 et Er
est en
et Er
est en 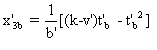
Les vitesses respectives de Or et Er sont alors : 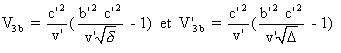
Dans S3 , líextrémité de la règle nía pas même vitesse que líorigine.
b) Déterminons la longueur de la règle à la date t3 de S3
Cette
longueur est soit 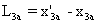 , soit
, soit 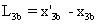 , selon que Or se trouve en x3a
ou en x3b .
, selon que Or se trouve en x3a
ou en x3b .
On trouve
: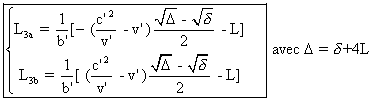
Les longueurs
sont données en fonction de t3.
On remarque
que si L=0, alors L3a = L3b
= 0 , et que L3a et L3b
tendent vers -L/b' lorsque t3 tend vers
plus l'infini si v'>0,
vers moins l'infini si v'<0.
Serge CABALA