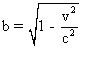
On a
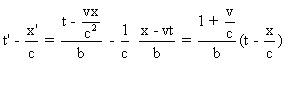 et
et 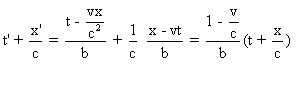
Si l'on pose :
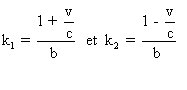 ,
,
on trouve que :
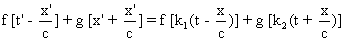 ,
,
ce qui prouve que la nouvelle expression est une onde transversale possible de la bande élastique.
1° On pose 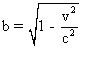
On a 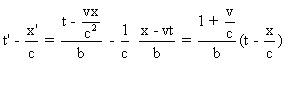 et
et 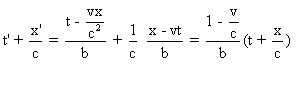
Si l'on pose : 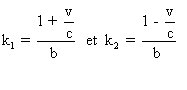 ,
,
on trouve que :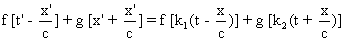 ,
,
ce qui prouve que la nouvelle expression est une onde transversale possible
de la bande élastique.
2° Dans cette question on suppose f périodique
bornée.
C'est à dire qu'il existe deux constantes
réelles r et s telles que pour tout t, r<f(t)<s
.
Le point d'abscisse xo
est point fixe si et seulement si 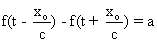 , a réel constant indépendant de t.
, a réel constant indépendant de t.
Nous allons prouver que a=0 .
En remplaçant t par 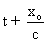 dans l'expression du point fixe, on trouve que pour tout t,
dans l'expression du point fixe, on trouve que pour tout t, 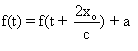 .
.
En remplaçant t par 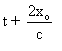 dans la dernière expression obtenue, puis en recommençant,
dans la dernière expression obtenue, puis en recommençant,
on trouve que pour tout entier naturel
n : 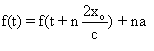 .
.
Si a est différent de zéro,
na tend vers plus ou moins l'infini, ce qui est impossible car f est bornée.
Donc a=0 .
Les points fixes ont donc pour ordonnée
zéro. Ils vérifient pour tout t :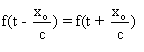 .
.
En remplaçant t par 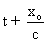 , on trouve que pour tout t ,
, on trouve que pour tout t , 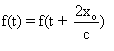 .
.
Donc 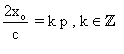 , p étant la période de f. On a donc :
, p étant la période de f. On a donc : 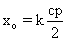 .
.
La distance entre deux points fixes
consécutifs est : 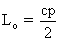 .
.
3° Le point d'abscisse 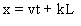 a
pour ordonnée zéro quelque soit t ,
a
pour ordonnée zéro quelque soit t ,
si et seulement si pour tout t : 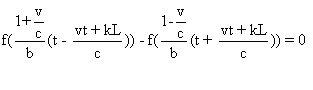 .
.
Soit si et seulement si pour tout t , 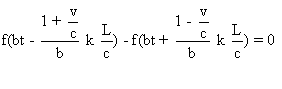
Soit encore si et seulement si pour tout T
, 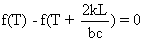 en posant
en posant 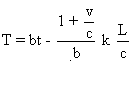 .
.
On a donc 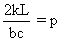 ,
ce qui donne
,
ce qui donne 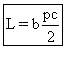 .
.
La distance entre deux points "fixes" consécutifs
est maintenant: 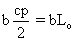 .
.
Les points fixes se déplacent à vitesse
v .
4° Montrons, avant d'aborder les questions, que la période de battement de l'onde (O) est bien p.
C'est à dire que p est la plus
petite valeur strictement positive
qui vérifie: 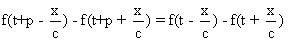 , pour tout t, tout x .
, pour tout t, tout x .
Soit p' une valeur différente
de zéro qui vérifie la même propriété
que p.
Pour tout x,t on a: 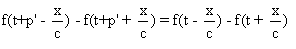 .
.
Remplaçons t par 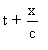 dans
la dernière expression.
dans
la dernière expression.
On a: 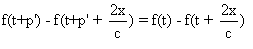 .
Fixons t=0 .
.
Fixons t=0 .
Pour tout x on a: 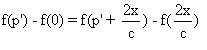 .
.
En posant a=f(p')-f(0) , et en remplaçant
2x/c par x (ce qui est possible car l'égalité est vraie pour
tout x ) ,
on a : 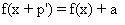 .
.
Puisque f est bornée, d'après
ce qui a été fait dans la question 2° , on a:
a=0 .
p' est un multiple de p. p est bien
la période de battement de l'onde (O) .
a) L'origine du repère Sv
a pour équation horaire dans S: x=vt .
Si E est un événement
de coordonnées (x, t) dans S , les coordonnées de
E dans Sv sont (xg,t) avec x=vt+xg
.
Par rapport à
Sv, l'équation de l'onde (O)
est donc: 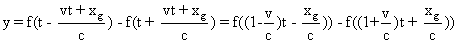
Toujours par rapport
à Sv , l'équations de l'onde (Ov)
est: 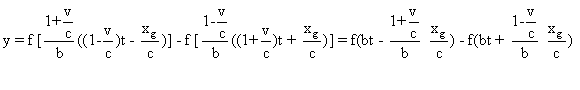
Or pour tout t, 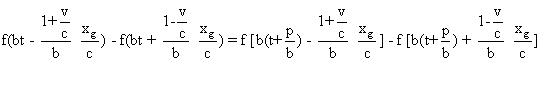
Ce qui prouve que la période
de battement de (Ov) par rapport à Sv est 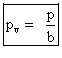
b) Soit xog un
point fixe, par rapport à Sv, de l'onde (Ov) .
Cela signifie que pour tout
t : 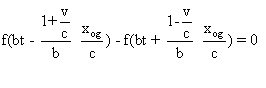 .
.
En posant : 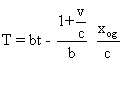 ,
on trouve que pour tout T ,
,
on trouve que pour tout T , 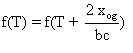 .
.
On a donc: 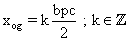 .
.
On retrouve, comme dans
la question trois, que la distance entre deux points fixes consécutifs
est bpc/2 .
5° Les transformations recherchées sont de la forme
x’=mx+nt+p , t’=st+rx+q .
m,n,p,s,r,q étant des constantes.
Un théorème
résume l'étude de cette cinquième question.
Ces transformations conviennent si et seulement
si t’-x’/c et t’+x’/c sont de la forme
k(t-x/c)+e ou k(t+x/c) +e , k,e constantes.
Or on a: 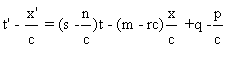 , et
, et 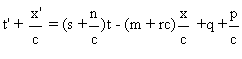
a) s-n/c=0 alors m-rc=0 aussi pour que
t’-x’/c soit de la bonne forme.
On trouve alors que 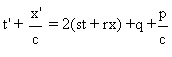 .
.
s = 0 entraîne r =
0 ce qui donne m = n = 0 .
Le cas 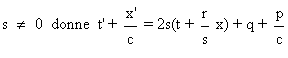 .
.
C’est de la bonne forme
si et seulement si 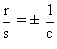 , et dans
ces cas,
, et dans
ces cas, 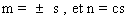 .
.
On a : 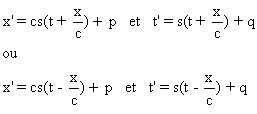
b) s+n/c=0 . On retrouve les mêmes
formules que ci-dessus par un raisonnement analogue.
c) 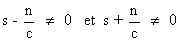
Dans ce cas on a : 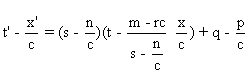
et 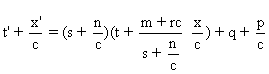
Ces écritures sont
de la bonne forme si et seulement si 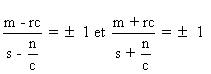
Cas1) 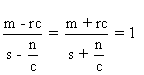 .
On a:
.
On a: 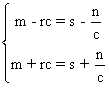 ce qui entraîne
ce qui entraîne 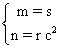
On trouve que x'=sx+rc2t+p et t'=st+rx+q . Si s=0 alors r =0
. Supposons s non nul.
On a alors 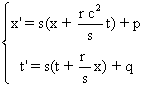 Posons
:
Posons
: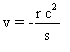 , ce qui donne
, ce qui donne 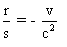 .
.
On obtient : 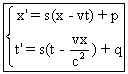 s et v étant
des constantes quelconques (s=0 convient aussi ici).
s et v étant
des constantes quelconques (s=0 convient aussi ici).
Dans le cas où s est non nul , posons d=1/s . On obtient 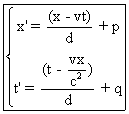
Cas 2) 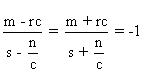 .
Par un raisonnement analogue au Cas 1) ,
.
Par un raisonnement analogue au Cas 1) ,
on trouve que 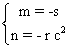 , ce qui donne
, ce qui donne 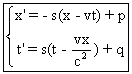 s et v quelconques.(s=0 convient)
s et v quelconques.(s=0 convient)
Lorsque s et non nul, posons d=-1/s , on a 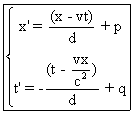
Cas 3) 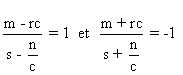 .
On trouve
.
On trouve 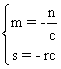
ce qui donne : 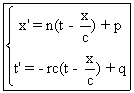 n , r constantes
quelconques.
n , r constantes
quelconques.
Cas 4) 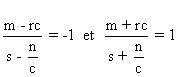 .
On trouve que
.
On trouve que 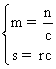
ce qui donne : 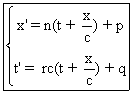 n , r constantes
quelconques.
n , r constantes
quelconques.
L'ensemble des résultats de cette question
5° se résume dans le théorème suivant.
Théorème
Des transformations linéaires de x et t transforment
toute onde sur une ligne en une nouvelle onde sur cette même ligne,
si et seulement si elles sont d'un des types
suivants: 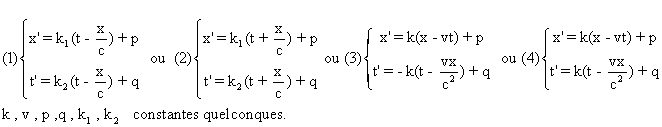
k peut dépendre de v .
Lorsque k est non nul , on peut poser k=1/d
. En prenant k = 1/b , le groupe (4) donne les transformations de Lorentz.
On remarque que les t' dans (3) et (4) varient
en sens contraires.
Etudions le comportement des points fixes et des battements.
Soit 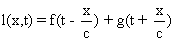 une onde quelconque, l(x',t')
l'onde transformée par une
une onde quelconque, l(x',t')
l'onde transformée par une
des transformations précédentes.
*)Les transformations (1) et (2) ne fournissent en général
aucun point fixe, ou alors tout point devient fixe
pour certaines fonctions l(x,t) et certains choix des constantes.
Ces transformations présentent peu d'intérêt.
*)Prenons les transformations (4) avec k non nul. Posons k=1/d .
Pour simplifier, on prend p=q=0 dans les transformations (4).
De plus on suppose que x=0 est un point fixe de l(x,t).
On a donc: 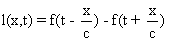
On suppose aussi que f est périodique bornée de période
p.
La période de battement de l(x,t) est p , la distance entre deux
points fixes consécutifs de l(x,t) est
Lo=pc/2 (voir questions précédentes).
Des calculs analogues à ceux de la question 4°, dans
lesquels on remplace b par d donnent :
Les points fixes de l(x,t) se transforment dans l(x',t') en points "fixes"
qui se déplacent à vitesse v le long de Ox .
La distance entre deux points "fixes" consécutifs de l'onde l(x',t')
est
L = |d|L0 . |d| désignant la valeur
absolue de d.
La période de battement de l(x',t') ( dans le repère Sv
) est 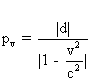 .
.
Remarque: si |v|=c , les transformations (3) et (4) deviennent (1) ou (2)
.
*)Prenons les transformations (3) avec k non nul.
On a en posant k=1/d , 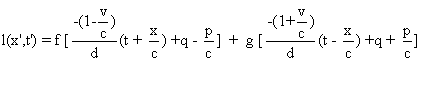
Pour simplifier, on prend p=q=0 .
On prend le même l(x,t) que précédemment.
On a ainsi : 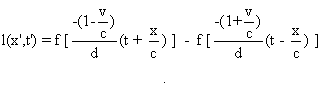
Par des calculs analogues à ceux de la question 4°,
On trouve que x=vt est point fixe de l(x',t') , que la période pv
de battement de l(x',t')
est 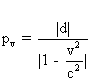 , et que la distance entre
deux points fixes consécutif est L=|d|Lo
.
, et que la distance entre
deux points fixes consécutif est L=|d|Lo
.
Nous obtenons les mêmes résultats qu'avec les transformations
(4).
Serge CABALA.