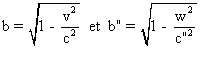Réponses aux exercices sur les transformations de Lorentz


Home page           Retour au choix

Exercice 3

            Dans cet exercice je pose :  .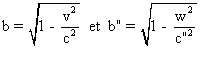
            Je rappelle que -c<v<c ; et que -c"<w<c"
            Les notations yg' et yg" seront remplacées par tg' et tg" , ce qui fait mieux penser au temps.

1° a) On a : 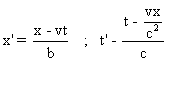 . Et on a : .
     b) On trouve : .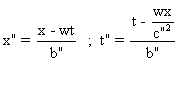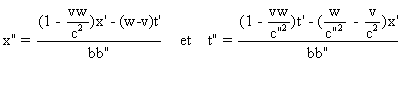

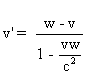    Ces formules s'obtiennent en exprimant x et t en fonction de x' et t' que l'on remplace ensuite dans les expressions de x" et t" .
    On remarque que si c"=c , et que si l'on pose  , alors on a :

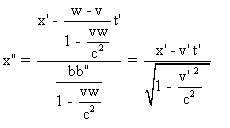    et .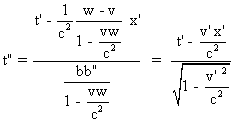

    On retrouve les formules classiques de passage de S' à S" , v' étant la vitesse de S" par rapport à S' .
    En permutant les rôles de v , w ; c , c" ; x' , x" ; t' , t" , on obtient les formules donnant
    x' et t' en fonction de x" et t" .

    Soit :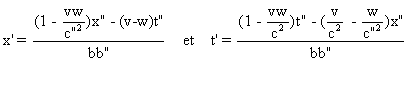 
     

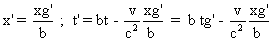
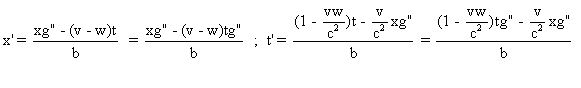
     c) Puisque Sg' et Sg" sont des systèmes galiléens classiques, on a :
         xg' = x - vt , yg' = tg' = t .
         xg" = x - wt , yg" = tg" = t .
         Ce qui donne :     
          (x', t') est donné ici en fonction de (xg' , tg')
          On trouve de même (x', t') en fonction de (xg", tg") .
          

2°   a) La vitesse de S' par rapport à S" est obtenue en faisant x'=0 dans les expressions de x" et t" en fonction de x' et t' ,
           puis en exprimant x" en fonction de t" .
           On obtient : 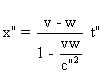. La vitesse de S' par rapport à S" est donc de : .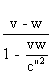
          La vitesse de S" par rapport à S' est de :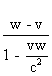 
           Ces deux vitesses sont opposées si et seulement si c"=c (pour v différent de w et tous deux différents de zéro).
           On peut se demander si ces deux vitesses peuvent être égales lorsque v et w sont différents.
            La réponse est oui pour certaines valeurs de c , c" , v , w . Pour cela ,on se donne c et v , v non nul avec -c<v<c .
            On prend c" quelconque dans l'ensemble 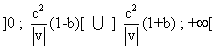 puis on prend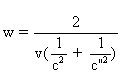 
            Le choix de c" doit être tel que le w obtenu vérifie -c"<w<c" .
            Exemple : c = 5 ; v = 4 . Ce qui donne b= 3/5 . On doit prendre 0<c"<5/2 ou c">10
            On prend c"=2 ce qui donne w=50/29 . La vitesse de S' par rapport à S" est de -22/7 ,
            vitesse égale à celle de S" par rapport à S' .

         b)   La question est ici une simple question de mécanique classique. Sg' est un système galiléen.
               La vitesse de S" par rapport à Sg' est donc w-v .
               La vitesse de S' par rapport à Sg" est v-w car Sg" est galiléen.
               Les deux vitesses sont toujours opposées.
               Cette question ne présente aucune difficulté, mais on peut être troublé par les questions précédentes.

3°       On a :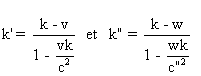 
          On trouve :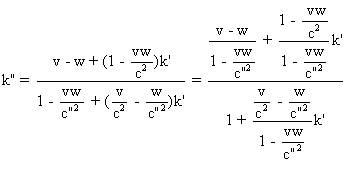 

                            

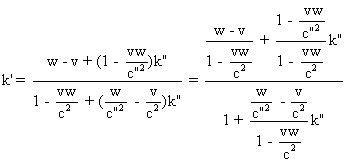
4°      D'après l'exercice 2 , 4°, a) , on trouve :  .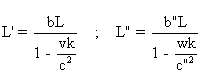
         Ce qui donne :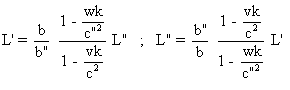 
         L'=L" si et seulement si : .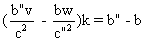
         Si 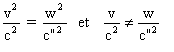 , on a  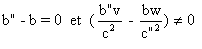. k n'existe pas .
         Si w = v = 0 , on a L'=L" pour toute valeur de k (S , S' et S" sont confondus ).
         Si w = v et c" = c , de façon évidente L'=L" pour tout k ( S' et S" sont confondus ).
         Dans tous les autres cas on doit prendre 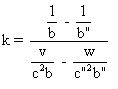 pour avoir L'=L" .
        Remarque : Si c" = c , on a .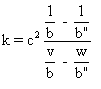
       Ce qui peut encore se mettre sous la forme 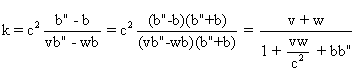 ( c" = c ici ).

       Montrons que -c<k<c lorsque c" = c .
       Si 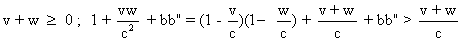 donc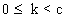 
      Si 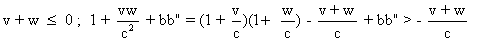donc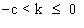 
      On a donc toujours -c<k<c .
       Dans le cas où c" = c , supposons que l'on passe de S à la règle R par les transformations de Lorentz
       de constantes c et k ce qui est possible car -c<k<c .
       La vitesse de S' par rapport à R est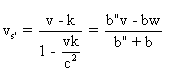 
       La vitesse de S" par rapport à R est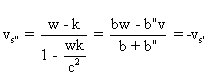 
       Ces deux vitesses sont opposées. L'=L" devient ainsi évident pour cette vitesse k.

       Exemple prenons c = c" = 5 ; v = 3 et w = 4 . On trouve k = 25/7 .
       Si on suppose que l'on passe de S à la règle à l'aide des transformations de Lorentz de constantes " c = 5 et k = 25/7 " ,
       on trouve que la vitesse de S' par rapport à la règle est -1 , et que la vitesse de S" par rapport à la règle est 1 .

 

5°   Soient (x',t') les coordonnée de E1 dans S' . Les coordonnées de E2 dans S' sont (x'+5,t') ,
       car E1 et E2 sont simultanés dans S' .
       D'après la première question b) la date de E1 dans S" est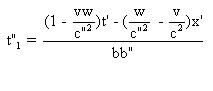 
       La date de E2 dans S" est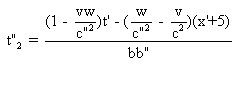 
       Ces deux événements sont simultanés dans S" si et seulement si t"1 = t"2 .
       Soit si et seulement si .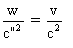
       On se donne c ; c" et v , et on prend .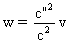
       La valeur w calculée convient si et seulement si -c"<w<c" . Soit si et seulement si  .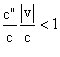
      Dans ce cas , et pour ce choix de w , deux événements quelconques simultanés dans S' restent simultanés dans S" .
      Remarque : si 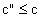, le w calculé convient toujours.

                                                                                     Serge CABALA .