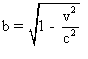
1° L’équation du mouvement de M par rapport à S étant x = kt ,
Dans cet exercice l’énoncé stipule que 0<v<c . Je rappelle que: 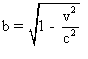
1° L’équation du mouvement
de M par rapport à S étant x = kt ,
en remplaçant x par kt dans les transformations
de Lorentz , puis en exprimant t en fonction de t' ,
on trouve que: 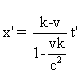 .
.
La vitesse de M par rapport à S’
est: 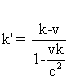 . La vitesse
k’ n’existe pas pour k = c2/v .
. La vitesse
k’ n’existe pas pour k = c2/v .
Dans ce cas, M est perçu comme étant
partout à la fois dans S’ à la date t’ = 0 .
Plus exactement, M passe en tout point d’abscisse
x’ de S’ lorsque l’horloge de S’ qui se trouve en x’ marque
zéro.
Le système S’ ne permet pas
une description cohérente de certains mouvements de M.
2° Le plus simple consiste à
préciser dans un tableau, les variations de k’ en fonction de k
.
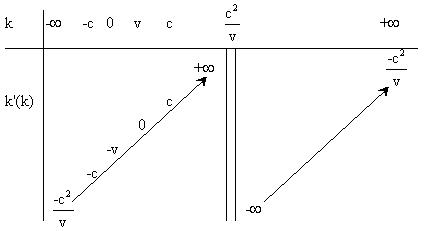
On remarque que lorsque k varie de c
à c2/v , k’ varie de c à plus l’infini.
Pour k supérieur à c2/v
, k’ est négatif . k et k’ sont de signes contraires pour tout k
compris entre 0 et v , et pour tout k > c2/v .
Lorsque k tend vers plus l’infini, k’
tend vers –c2/v , de même lorsque k tend vers moins l’infini.
Dans S’ , lorsque k > c2/v
, le mobiles M a une vitesse k’ négative, de plus,
M semble arriver avant d’être
parti. Les effets semblent précéder la cause.
Penser aux fuseaux horaires terrestres
et à l’avion Concorde. Cet avion arrive à New York à
une date locale inférieure à celle de départ de Paris.
S’ n’est pas un système
de référence toujours cohérent.
3° La troisième question est résolue
en même temps que la seconde. Se reporter au tableau de variation
de k’ .
Les limites de k’, lorsque k tend
vers plus ou moins l’infini sont égales à –c2/v
.
Remarque : lorsque k < c2/v
, dans S’ , M n’arrive jamais avant d’être parti.
4° a) L’origine de la règle
a pour équation horaire dans S : x = kt .
Son équation horaire dans S’ est : 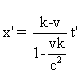 (
voir 1°) .
(
voir 1°) .
L’équation horaire de l’extrémité de la règle
dans S est x = kt + L .
En remplaçant x par kt + L dans les transformations de Lorentz,
puis en exprimant t en fonction de t’ ,
on trouve
: 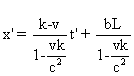 .
On a donc
:
.
On a donc
: 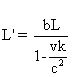
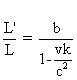 . La discussion
est résumée par le tableau de variation suivant de L’/L en
fonction de k .
. La discussion
est résumée par le tableau de variation suivant de L’/L en
fonction de k .
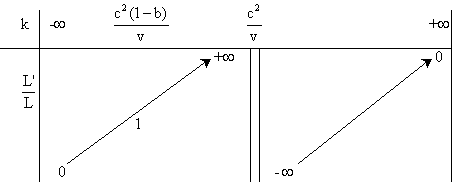
On remarque que L' devient infini au voisinage de c2/v .
c) Le tableau précédent permet de voir que L' tend vers zéro lorsque k tend vers l'infini.
5° Les valeurs de k pour lesquelles S'
reste cohérent vont de moins l'infini à c2/v exclu.
Les paradoxes apparaissent pour
les valeurs de k supérieures à c2/v .
6° Le mouvement de N dans S a pour
équation horaire : x = t2 .
A la date t de S, N est
en x = t2 .
Dans S' , N se trouve en 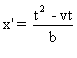 et l'horloge de S' qui se trouve en x' marque alors
et l'horloge de S' qui se trouve en x' marque alors 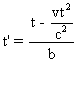 .
.
Calculons, lorsque cela est possible,
t en fonction de t' , ce qui se fait en utilisant la dernière équation.
On trouve : 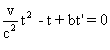 . Le discriminant, de cette équation en t , est
. Le discriminant, de cette équation en t , est 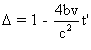 .
.
Le discriminant est positif ou
nul si et seulement si 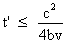 ( 0 < v < c d'après l'énoncé ).
( 0 < v < c d'après l'énoncé ).
Les seules valeurs affichées
par les horloges de S' lorsque N les croisera, sont celles inférieures
ou égales à c2/(4bv) .
Toute valeur supérieure
ne sera pas rencontrée par N .
Résumons dans un tableau
les variations de t' en fonction de t .
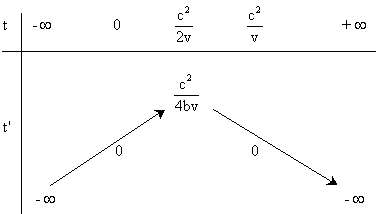
Ce tableau permet de se rendre
compte que toute valeur de t' inférieure à c2/(4bv)
sera toujours rencontrée deux fois par N au cours de son voyage.
Autrement dit: pour tout t' donné,
t'< c2/(4bv) , N croisera toujours deux horloges distinctes
de S' qui marqueront ce t' à l'instant du croisement. t'
< c2/(4bv).
Pour tout t'< c2/(4bv),
les deux valeurs distinctes correspondantes de t sont:
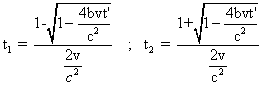 , et on a :
, et on a : 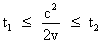 .
.
Le mouvement de N dans S' ne
peut pas se décrire à l'aide d'une seule équation
horaire.
On a une première équation horaire
( x' exprimé en fonctions de t' ) lorsque t est inférieur
ou égal à c2/(2v) , et une seconde équation
pour t > c2/(2v) .
Ces équations horaires sont respectivement
: 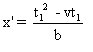 et
et 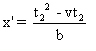
La première équation sera
appelée équation normale, la seconde paradoxale.
De façon plus détaillée,
Pour t< c2/(2v) , la relation
qui lie x' et t' , ou encore équation horaire normale du mouvement
de N dans S' , est :
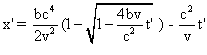 ( Equation normale )
( Equation normale )
Pour t> c2/(2v) , la relation qui
lie x' et t' , ou encore équation horaire paradoxale du mouvement
de N dans S' , est :
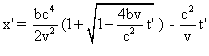 ( Equation paradoxale )
( Equation paradoxale )
La vitesse normale de N dans S' est
: 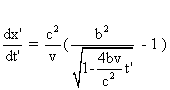 ,
pour t<c2/(2v).
,
pour t<c2/(2v).
La vitesse paradoxale de N dans S'
est : 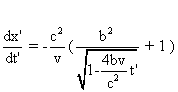 , pour
t>c2/(2v).
, pour
t>c2/(2v).
La vitesse paradoxale est toujours négative.
Durant la phase paradoxale de son mouvement
dans S', N semble toujours arriver avant d'être parti, d'où
la dénomination.
Les variations des vitesses normales et paradoxales en fonction de t' sont résumées dans les tableaux suivants.
Vitesse normale
Vitesse paradoxale
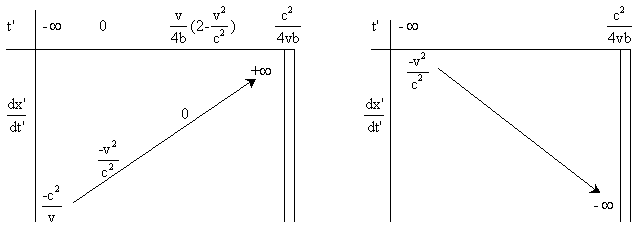
On remarque que t'=c2/(4vb) correspond à t=c2/(2v)
, et la vitesse de N par rapport à S est alors c2/v
, vitesse qui est celle à partir de laquelle apparaissent les paradoxes
dans S' (voir les questions précédentes).
Serge CABALA