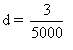Cette correction correspond à l'énoncé actuel.
Il est conseillé de relire les précisions données au début de l'exercice 1.

a) Rappel : 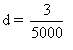. La relation entre g et s est donnée juste après avoir traité -a)

Refaisons les questions a),b),c) de l'exercice 4.

-a) En utilisant les nouvelles unités dans R_l et en s'aidant des résolutions des exercices 4 et 5 ,
on trouve : (A6)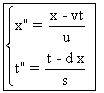, ce qui donne : (B6)

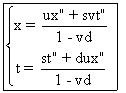
Exprimons (x",t") en fonction de (x',t') . Je rappelle que : 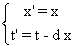 , formules donnée dans l'exercice 1.

En s'aidant de ce rappel, on trouve que :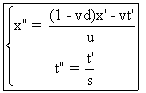 

Déterminons le nombre g d'heures de S_u (heures réelles) que contient une unité de R_l .

Pour cela, comme dans le complément de l'exercice 4 a), suivons le cadran solaire qui se trouve en Or origine de R_l .
L'équation du mouvement de Or par rapport à S_u est x = vt .
Remplaçons, dans la seconde équations de (A6), x par vt .
Nous obtenons: .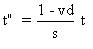
Prenons t"=1 ce qui donne pour t le g demandé, soit : 
Si v = 0, on a g = s .

-b) L'équation horaire du mobile M dans S_u est x = kt . En utilisant (B6) ,

on trouve que : 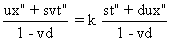, ce qui donne : (C6)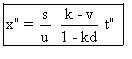

La vitesse k" de M dans R_l est alors : .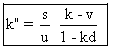

Les discussions se conduisent de manière analogue à celles faite en b) dans l'exercice 4.
Il faudra de plus tenir compte du signe de s/u .

Donnons l'équation horaire de M dans R_l en fonctions de k' , vitesse de M dans S_l .
En utilisant le fait que 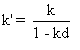, ce qui donne 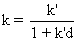, on trouve, en remplaçant dans (C6),
k par son expression en fonction de k', que :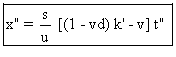 

-c) En procédant comme dans c) de l'exercice 4, on trouve que : 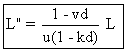, résultat indépendant de s, et identique à celui trouvé dans l'exercice 5.

L'expression de L" en fonction de L' est : 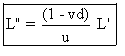, résultat également identique à celui de l'exercice 5.

b*) On a (A6)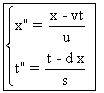que l'on compare à : (L)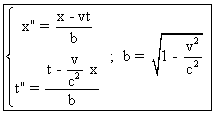

Pour que (A6) soit de type (L), il faut q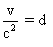ue : , et que .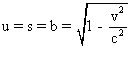

Cas 1  .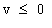
Dans ce cas c n'existe pas, car d est une constante strictement positive (d=3/5000).

Cas 2 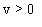. On prend, 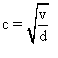, ce qui donne : .
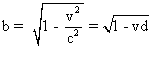On remarque que b existe et est non nul, si et seulement si vd < 1 , ce qui est réalisé si et seulement si 0<v<1/d .
Dans ce cas on trouve que : 0<v<c<1/d .
Puis on prend u = s = b. Lorsque s = b on a g = 1/b.
Les transformations (A6) deviennent ainsi des transformations de Lorentz de constantes v, c.
On passe de S_u à R_l par les transformations de Lorentz de constantes v, c. Avec 0<v<c .
Dans les transformations de Lorentz ainsi obtenues, c, u et s sont calculés à partir de v.
c n'est pas une constante indépendante de v.
Pour v donné, 0<v<1/d, le choix de u, s et c est unique.

Complément. En plus de modifier les unités de longueur et de temps dans R_l , modifions les aussi dans S_u .
Soit u₁ la nouvelle unité de mesure dans S_u et soit s₁ la nouvelle unité de temps dans S_u .
La nouvelle unité de mesure vaut u₁ km , la nouvelle unité de temps vaut s₁ heures.
Notons (x, t), les coordonnées d'un événement quelconque, par rapport à S_u muni des unités habituelles.
Notons (x₁, t₁), les coordonnées de ce même événement, par rapport à S_{u ,} muni des unités u₁ et s_1.

Nous avons : 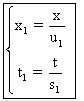soit : 

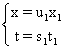
Soient (x₁, t₁) les coordonnées d'un événement E quelconque, dans S_u muni des unités u₁ et s₁.
Soient (x", t") les coordonnées de ce même événement E, dans R_l muni des unités u et s .

Nous avons : 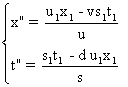 , soit : (A6')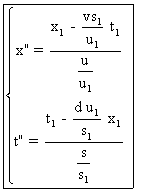

La question est la suivante : comment choisir u₁, s₁, u, s pour avoir des transformations de type (L).
Que valent alors les constantes v et c dans (L)?

Posons 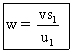(A6') s'écrit alors :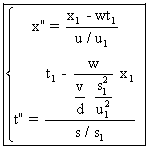 

w est la vitesse de Or , origine du système R_l , par rapport à S_u muni des unités u₁ et s₁.

Pour que ces dernières formules (A6') soient des formules du type formules de Lorentz, on doit avoir :
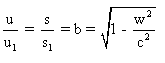avec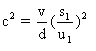 

Cas 1  .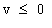
Dans ce cas c n'existe pas , car d >0 . v =0 donne c=0 qui ne convient pas aux formules (L).

Cas 2 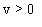. On se donne u₁ et s₁ de façon arbitraire ( u₁ et s₁ tous deux différents de zéro).
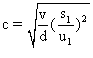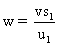On prend  et . On calcule b et on trouve, .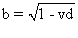
b existe et est non nul si et seulement si 0<v<1/d , et dans ce cas on a .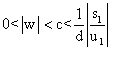
On calcule ensuite u et s. .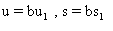
En prenant ces valeurs de v, u₁, s_1, u, s, w et c,
Les formules (A6') deviennent des transformations de Lorentz de constants w et c.
Dans les transformations de Lorentz ainsi obtenues, u₁ et s₁ sont arbitraires.
w, c, u et s sont calculés à partir de v, u₁ et s₁ .
Pour v, u₁ et s₁ donnés, w, c, u et s sont uniques.
En faisant varier u₁ et s₁ , tout en gardant v, on obtient différentes valeurs de w et de c, b restant constant.
(v est la vitesse en km/h de Or par rapport à S_u .)

Les unités choisies dans S_u déterminent de façon unique celles que l'on doit choisir dans R_l ,
pour que l'on passe de S_u à R_l par des transformations de Lorentz.