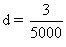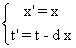Je rappelle que 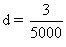. On sait d’après l’exercice 1, que .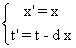

a) De façon évidente on a , 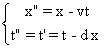 soit : (A) .

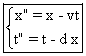Donc : (B) .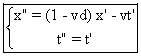

Complément: Déterminons le nombre d'heures de S_u (heures réelles), contenues dans une unité de temps de R_l.
Pour cela, suivons le cadran solaire qui se trouve en Or.

Par rapport à S_u, l'équations du mouvement de Or est x = vt.
Remplaçons x par vt dans (A), nous obtenons : .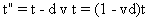
Pour t"=1 on obtient : 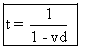. On suppose 1-vd non nul.
Lorsqu'il s'écoule une heure (une unité) dans R_l , il s'écoule 1/(1-vd) heures dans S_u.

Remarque : si 1-vd>0, les cadrans solaires de S_u et R_l tournent dans le même sens, sinon ils tournent en sens contraires.
Pour 1-vd<0, les cadrans solaires de R_l vont en régressant.

Exemple : prenons v = 2500/3 = 833.333... On a 1/(1-vd) = 2.
Lorsqu'un cadran solaire de R_l avance d'une unité (avance d'une heure), il s'écoule deux heures dans S_u (deux heures réelles).

b) L’équation du mouvement de M dans S_u est x=kt .
On remplace x par kt dans (A) ce qui donne :  .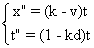
On élimine t entre ces deux équations et on trouve ainsi l’équation du mouvement de M dans R_l .
                                              Soit : (C).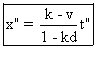

On constate que la vitesse k" de M par rapport à R_l est :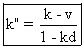 

Discutons de cette vitesse k" en fonction de v et de k.

Cas1 ) 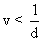 La dérivée de k" par rapport à k et positive.
La discussion est résumée dans le tableau ci-dessous.

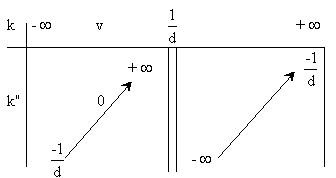
Lorsque k>1/d , on a k"<0 . La description du mouvement de M dans R_l est alors paradoxale.
Le mobile semble arriver avant de partir.

Cas 2 )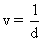 
Dans R_l le temps semble figé. Aucune horloge de ce repère (cadran solaire) ne varie.
L'horloge (cadran solaire) de R_l placée en Or (origine du repère R_l ) marque toujours zéro.
Celle placée en x"=1 marque toujours –d , celle en x"=2 marque toujours –2d etc.

L'équation du mouvement de M dans R_l
devient : 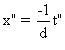 , équation qui ne dépend plus de k.
Cette équation est l'équation du déphasage des horloges de R_l .

Cas 3 ) 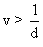 La dérivée de k" par rapport à k est maintenant négative.
La discussion est de nouveau résumée dans le tableau ci dessous.

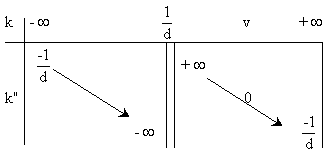
Le mouvement de M dans R_l a une description paradoxale. Lorsque k augmente, k" diminue toujours.
De plus, pour tout ,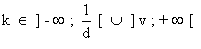
le mobile semble dans R_l arriver avant partir.

Donnons maintenant, l'équation du mouvement de M dans R_l en fonction de son équation dans S_l,
plus précisément en fonction de k', vitesse de M par rapport à S_l .

Soit x'=k't' l'équation du mouvement de M par rapport à S_l .
Remplaçons x' par k't' et t' par t" dans (B) donné au début de cet exercice.
On obtient : 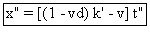 ce qui est la réponse demandée.
Remarque : D'après l'exercice 2 , on a :  .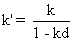
Si on remplace, dans la dernière formule encadrée, k' par cette dernière expression, on retrouve (C) .

c) R2 se déplace à vitesse k par rapport à S_u .
Soit x=kt , l'équation par rapport à S_u , de son origine Or2.
L'équation de sont extrémité Er2, par rapport à S_u est alors x=kt+L .
D'après (C) , l'équation de Or2 par rapport à R_l est :.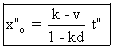
L'équation de Er2 s'obtient en remplaçant x par kt+L dans (A) ,

ce qui donne : 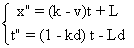 . On exprime t en fonction de t" :  .

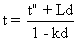Puis on remplace t par cette dernière expression dans la première équation du système ci-dessus.

On a ainsi : 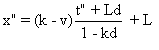 . Soit :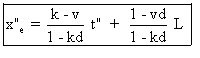 
La notation x"_e précise qu'il s'agit de l'équation du mouvement de l'extrémité Er2 de la règleR2.
La longueur L" de la règle R2 par rapport à R_l est donc :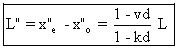 

Exprimons L" en fonction de L' et k' .
D'après l'exercice 3 on a : 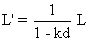 . Donc :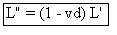 
On remarque que l'expression de L" en fonction de L' est indépendante de k' (et de k) .
Quelque soit la vitesse de R2 , L"/L' est constant.
Le rapport ne dépend que de la vitesse v de la règle R.