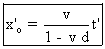Rappel : d=3/5000.

a) Dans S_l , l'équation de l'origine de la règle est :  .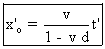

L'équation dans S_l de l'extrémité de la règle s'obtient en remplaçant x par vt+L dans les équations (1) de l'exercice 1 .

On obtient : 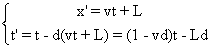 , ce qui donne,  ,

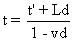et enfin :  .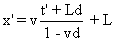
(Formule qui est l'équation horaire dans S_l , de l'extrémité de la règle R.)

En réarrangeant les termes de cette dernière équation, et en remplaçant x' par x'_e pour préciser qu'il s'agit de l'extrémité de la règle,

on trouve :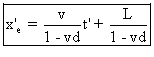 

La longueur de la règle dans S_l est donc de : 

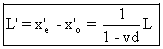
b) 
La règle tend à "s'évanouir" dans S_l ,lorsque sa vitesse par rapport à S_u tend vers moins l'infini.
L' reste positif lorsque v tend vers moins l'infini.

c) La discussion est résumée par le tableau suivant qui donne les variations de L' en fonction de v .

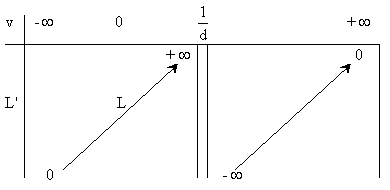
Je rappelle que :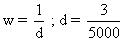 

Lorsque v tend vers w , avec v<w , L' tend vers plus l'infini.
Lorsque v dépasse w , L' devient négatif .
La mesure de la règle, suivant nos définitions, donne dans S_l , un résultat négatif lorsque v>w .

Expliquons ce paradoxe.
Lorsqu'un observateur fixe O_e de S_l voit passer l'extrémité de la règle tandis que son cadran solaire indique une date t'_o , le seul autre observateur fixe O_o de S_l qui verra passer devant lui l'origine de la règle lorsque son cadran solaire marquera la même date t'_o se trouve après O_e .
Lorsque v>w , ou égale à w , la description du mouvement de la règle dans S_l devient paradoxale.
Le système S_l ne permet pas une descriptions cohérente de certains phénomènes, contrairement à S_u .