Ce que je fais ici est tout à fait nouveau pour un scientifique traditionnel (relativiste ou non).
La cinématique que je développe dans un cadre très classique fait entièrement appel aux temps locaux.
Cette cinématique nouvelle permet de beaucoup mieux comprendre la signification des transformations de Lorentz,
et surtout, permet une généralisation et une interprétation de ce genre de formule.

Les exercices utilisent les fuseaux horaires, car c'est avec eux que l'on saisit le mieux la véritable signification de temps local.

Dans les textes sur la relativité on rencontre parfois le terme de temps local, mais jamais l'analogie avec les fuseaux horaires.
En relativité, le terme de temps ou temps local, est perçu comme une sorte d'entité quasi divine
qui entretient des relations mystérieuses (bien que mathématiques) avec son proche espace.
La nouvelle cinématique explique et clarifie complètement la situation.

Tout d'abord quelques précisions sur les cadrans solaires utilisés pour mesurer les temps dans les divers systèmes de références utilisés dans les exercices sur les fuseaux horaires.

Les cadrans solaires sont gradués en heures.
Tout cadran solaire immobile sur notre équateur théorique, a son affichage qui avance d'une graduation chaque fois qu'il s'écoule une heure réelle.
C'est ces mêmes cadrans solaires (avec les mêmes graduations), qui sont utilisés dans tous les systèmes de références, immobiles ou mobiles par rapport à l'équateur.
Les cadrans solaires d'un système immobile avances tous d'une graduation, lorsqu'il s'écoule une heure dans le repère absolu de l'équateur.
Dans les systèmes en translations par rapport à l'équateur, les cadrans solaires se déplacent et n'avancent pas d'une graduation lorsqu'il s'écoule une heure dans le repère absolu de l'équateur.

Si le système se déplace dans le sens positif (du coté de l'ouest, et sans dépasser la vitesse apparente du soleil), ses cadrans solaires avancent de moins d'une graduation lorsqu'il s'écoule une heure dans le repère absolu de l'équateur.

Si le système se déplace dans le sens négatif (du coté de l'est), ses cadrans solaires avancent de plus d'une graduation lorsqu'il s'écoule une heure dans le repère absolu de l'équateur.

L'unité de temps prise en un point fixe d'un système en mouvement est toujours données par l'intervalle de deux graduations consécutives du cadran solaire qui se déplace avec ce point.
(Le cadran solaire considéré est fixe par rapport au système en mouvement.)
L'unité de temps du système en mouvement est encore appelée heure.
Lorsque le système se déplace dans le sens positif (sans dépasser la vitesse apparente du soleil), une heure du système en mouvement correspond à plus d'une heure du repère absolu.
Lorsque le système se déplace dans le sens négatif, une heure du système en mouvement correspond à moins d'une heure du repère absolu.
Précision supplémentaire : tout cadran solaire d'un système en mouvement donne toujours la même indication que le cadran solaire fixe de l'équateur sur lequel il passe.

Changer l'unité de temps d'un système (fixe ou en mouvement) c'est re graduer tous ses cadrans solaires.
Une nouvelle graduation sera formée de s anciennes, s réel quelconque strictement positif (de préférence).

L'exercice 1 est particulièrement court.

Le décalage horaire étant de 12 heures pour 20000 kilomètres, il s'ensuit qu'il est de 12/20000 d'heure par km.
Soit de 3/5000 d'heure par km.

Les formules de passage de S_u à S_l sont : (1)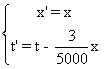

Celles de S_l à S_u sont :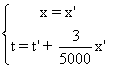 

Dans tous les exercices qui suivent, on posera :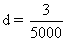 

Remarque:
Si l'on veut généraliser les formules obtenues dans les exercices, d peut prendre une valeur quelconque, ou même dépendre d'autres variables.