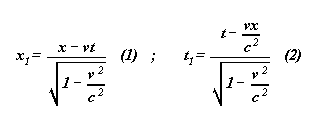
Par une étude inédite, purement mathématique et très élémentaire, je démontre :
 

Que les transformations de Lorentz sont interprétables dans un espace temps classique (euclidien),
Qu'elles admettent des représentations mécaniques naturelles fondamentales,
Que ces transformations n'excluent pas les transformations de Galilée,
Que les vitesses plus grandes que c, c vitesse limite d'utilisation des formules de Lorentz ,
        ne sont pas exclues par ces transformations,
Que le principe de relativité d'Einstein n'est pas conséquence de ces transformations.
 
 

Début de l'étude.

Par simplification les formules ne sont étudiées ici que dans un espace à une dimension .
Soit S un axe Ox , S₁ un axe O₁x₁
S₁ est parallèle à S et S₁ glisse sur Ox à la vitesse constante v ,
v vérifiant -c < v < c , c constante positive donnée.
Cela signifie que le mouvement de O₁, origine de S_1, est déterminé dans S, par l'équation x = vt + x_{o .}

Par un choix adéquat de l'origine O de S , nous pouvons toujours avoir x_o=0 .
Nous prendrons donc comme équation du mouvement de O₁ par rapport à S , l'équation x = vt

Si E est un événement de coordonnées (x,t) dans S , les coordonnées (x₁ ,t₁ ) de E dans S₁ sont
par définition des transformation de Lorentz: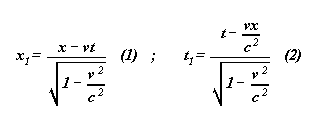

Etant donné les deux systèmes S et S_{1 ,} on dit que l'on passe de S à S₁ par les transformations de Lorentz de constante c .
Dans ce qui suit on pose: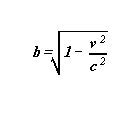, b est une constante qui ne dépend que de v , b vérifie :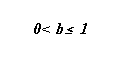( c reste fixe )  
                                                                                page 1

Autre expression de t₁

D'après (1) on a : x = vt + bx₁ .
Remplaçons x par cette expression dans (2) , nous obtenons :

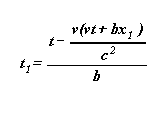Soit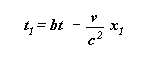 
Cette dernière formule permet de nous rendre compte :

1°) Du ralentissement des horloges de S₁ suivant le facteur multiplicatif b ,
2°) Du déphasage des horloges de S₁ suivant le terme additif 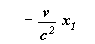terme proportionnel à x₁ .
De plus La formule x = vt + bx₁ comparée à la formule de transformation galiléenne
x = vt + x₁ , permet de se rendre compte d'un raccourcissement des longueurs de S₁ suivant la direction Ox , toujours suivant le facteur multiplicatif b .

Dans ce qui suit , je vais représenter les systèmes S et S₁ en donnant à c et v des valeurs numériques assez faibles, valeurs qui permettent de faire des figures très explicites. Ces figures jamais vues,  permettrons de saisir pleinement la signification des formules de Lorentz.
 

Représentation de S et de S₁ dans le cas particulier où :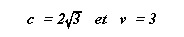 

Avec ces valeurs , on obtient c² = 12 et b = 1/2 , ce qui donne pour x₁ et t₁ :
 
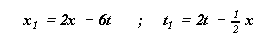
Soit encore :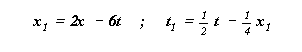
L'unité de longueur dans S est prise égale à 2 centimètres . Ces différentes valeurs permettent de visualiser commodément les systèmes S et S₁ à différentes dates t de S . (Voir les axes de la figure 1)

Les différents dessins de la figure 1 sont obtenus de la manière suivante.

Pour le dessin 1, on fait t=0 , et on donne à x toutes les valeurs possibles dans les formules

                           x₁ = 2x - 6t ; t₁ = 2t - 1/2 x .
Avec t = 0 , on a donc : x₁ = 2x et t₁ = - 1/2 x
Par exemple pour x = - 1 , on obtient : x₁ = -2 et t₁ = 1/2 .

Cela signifie que le point de S₁ en coïncidence avec le point de S d'abscisse - 1 , (à la date t = 0
de S ) a pour abscisse x₁ = -2 , et que l'horloge de S₁ qui se trouve en ce point , indique + 1/2
( +1/2h pour signifier que le nombre lu est une date) .

                                                                                page 2

De même pour x = 1/2 (toujours avec t = 0 ) , on obtient x₁ = 1 et t₁ = - 1/4 ( - 1/4h ) .
Le point de S₁ en coïncidence avec le point de S d'abscisse +1/2 (dans S ) , a pour abscisse 1
(Dans S₁) , et l'horloge de S₁ qui se trouve en ce point , indique - 1/4 (- 1/4h ) .
On procède de même pour toutes les autres valeurs de x, toujours avec t = 0 , ce qui donne le système
S₁ vu de S à la date t = 0 de S. (Dessin 1 de la figure 1)

Pour obtenir le dessin 2, on prend t =1 , ce qui donne x₁ = 2x - 6 et t₁ = 2 - 1/2 x , et on fait varier x
comme précédemment , ce qui donne le système S₁ vu de S à la date t = 1 de S .
On procède de même pour obtenir le dessin 3 en prenant t = 2 (dans S) , ce qui donne
                               x₁ = 2x - 12 et t₁ = 4 - 1/2 x .

Dans les dessins ne sont indiqués que les temps donnés par les horloges qui se trouvent aux abscisses entières des systèmes.
 
 
Les dessins de la figure 1 conduisent aux remarques suivantes:

1° Les unités de longueurs de S₁ (dans la direction de la vitesse) sont constantes , et plus petites que les unités de longueurs
de S . Dans le cas des dessins de la figure 1 , l'unité de S₁ (dans la direction de la vitesse) est la moitié de celle de S .

2° Dans S₁ , en chaque point , nous devons disposer d'une horloge , horloge qui sert à dater les événements qui se déroulent en ce point de S₁ .
Lorsque dans S₁ se déroule un événement au point d'abscisse x₁ de S₁ , la date dans S₁ de cet événement est donnée par l'horloge de S₁ placée en x₁ , et par celle là seulement. Ce qui est tout à fait comparable aux fuseaux horaires terrestre.
Un événement qui se passe à Paris est daté par le fuseau horaire parisien, et non pas celui de Moscou.
 

Exemple: Sur le premier dessin, E₁ représente un certain événement (explosion par exemple).

E₁ se déroule dans S au point d'abscisse x = 1 , et l'horloge de S qui se trouve en ce point marque alors
la date t = 0 . Les coordonnées de cet événement dans S sont x = 1 et t = 0 .

Ce même événement se déroule dans S₁ au point d'abscisse x₁ = 2 et à la date t₁ = - 1/2 , date donnée par l'horloge de S₁ qui se trouve au point d'abscisse x₁ = 2 de S₁ . ( Voir figure 1);
 

3° Les événements simultanés dans un système ne le sont plus dans l'autre.
Définissons d'abord ce que sont deux événements simultanés dans un système.

Deux événements (explosions par exemple) sont simultanés pour un système , si et seulement si les
dates données par les deux horloges du système qui se trouvent aux endroits (aux coeurs) de ces
événements , indiquent le même nombre (donnent la même date).
 

Exemple: L'événement E₁ d'abscisse +2 dans S₁ et de date - 1/2 toujours dans S₁ ( événement indiqué
sur le premier dessin de la figure 1), et l'événement E₂ d'abscisse + 4 dans S₁ et de date - 1/2 , toujours dans S₁ (événement marqué sur le deuxième dessin de la figure 1) , sont simultanés par rapport à S₁ .

On remarque que les coordonnées de E₁ dans S sont x =1 et t = 0 , et que les coordonnées de
E₂ dans S sont x = 5 et t = 1 . E₁ et E₂ ne sont pas simultanés dans S .
 
De même deux événements simultanés dans S , n'ayant pas même abscisse , ne sont pas simultanés dans S ₁ .

Exemple: Sur le dessin n° 2 de la figure 1,
l'événement E₃ a dans S pour coordonnées x = 2 et  t = 1 .
L'événement E₄ a dans S pour coordonnées x = 4 et t = 1 .
E₃ et E₄ sont donc simultanés dans S .
Les coordonnées de E₃ dans S₁ sont x₁  = - 2 et t₁ = 1 .
Les coordonnées de E₄ dans S₁ sont x₁ = 2 et t₁ = 0 .
E₃ et E₄ ne sont pas simultanés dans S₁ .
                                                                                    page 4

Plus simplement , en se référant aux fuseaux horaires de la terre , une explosion qui se produit à Paris à midi , heure donnée par le fuseau horaire parisien , et une autre explosion qui se produit à New-York à midi , heure donnée par le fuseau horaire de New-York , forment deux événements simultanés selon le système de fuseaux horaires terrestres. Par rapport à un autre système de mesure des temps, ces deux événements ne sont plus simultanés.
 
 

4° La mesure de la vitesse d'un point mobile par rapport à un système de référence (en mouvement) doit faire appel à une définition plus précise que celle communément admise, définition qui doit exclusivement reposer sur les abscisses et les horloges de ce système de référence.

Définissons donc ce qu'est la vitesse d'un mobile par rapport à un système de référence.
La définition donnée l'est dans S₁ , mais demeure valable dans tout autre système.

Soit un mobile M se déplaçant sur l'axe S_1. M passe au point d'abscisse x₁ de S₁ à la date t₁
(date donnée par l'horloge de S₁ qui se trouve en x₁ ).

Puis M passe au point d'abscisse x'₁ de S₁ à la date t'₁ de S₁ ( date donnée par l'horloge de S₁ qui
se trouve en x'₁ ).

La vitesse moyenne du mobile par rapport à S₁ ,entre les points x₁ et x'₁ est :  (x'₁ - x₁)/(t'₁ - t₁)

La limite de cette vitesse moyenne lorsque x'₁ tend vers x₁ ( ou lorsque t'₁ tend vers t₁ ) donne la
vitesse exacte du mobile M au point x₁ de S₁ à la date t₁ de S₁ ( t₁ donné par l'horloge de S₁ qui se trouve en x₁ ).

Exemple : Reprenons nos dessins, (voir figure 2) . Soit M un mobile se déplaçant le long de l'axe

S₁, donc aussi le long de l'axe S . On suppose par simplification que la vitesse de M par rapport à l'axe immobile S est constante.

Sur le premier dessin de la figure 2, M se trouve en x₁ = 8 à la date t₁ = - 2 de S₁ (date donnée par l'horloge de S₁ qui se trouve en ce point ).

Sur le second dessin de la figure 2 , M se trouve en x'₁ = 0 à la date t' = 1/2 (date donnée par l'horloge de S₁ qui se trouve en ce point ).
 
La vitesse de M mesurée par rapport à S₁ est : (x'₁ - x₁)/(t'₁ - t₁) = (0 - 8) /(1/2 - (-2) ) = - 3.2 .
La vitesse de ce même mobile mesurée par rapport à S est - 1 .
 
Remarque : sur le troisième dessin de la figure 2 , les coordonnées de M par rapport à S₁ sont
x"₁ = - 8 et t"₁ = 3 .

Nous constatons que (x"₁ - x'₁)/(t"₁ - t'₁) = (x'₁ - x₁)/(t'₁ - t₁) = (x"₁ - x₁)/(t"₁ - t₁) = - 3.2
Ce qui permet de constater empiriquement que la vitesse de M par rapport à S₁ est constante.
 
Si M se déplace par rapport à S à la vitesse c (ou -c) , on peut constater expérimentalement sur les dessins que la vitesse de M par rapport à S₁ reste égale à c (ou -c) , à condition de faire les mesures comme dans le cas précédent. Je laisse au lecteur le soin de cette expérimentation éventuelle.

Je conseille de refaire les dessins des figures en prenant c = 5 , v = 4 ce qui donne b = 3/5 .
Les dessins , ainsi que la représentation de M qui se déplace à vitesse c , sont simples avec ces valeurs.
 
 
5° La mesure de la longueur d'un segment mobile par rapport à un système de référence (en mouvement) doit faire également appel à une définition beaucoup plus rigoureuse que celle donnée par  l'intuition, définition qui doit de nouveau reposer exclusivement sur les abscisses et les horloges de ce système de référence.

La définition est la suivante: Soit AB un segment de droite parallèle à S₁ , segment mobile ou immobile par rapport à S₁ .

L'origine A de AB passe au point d'abscisse x₁ de S₁ et l'horloge de S₁ qui se trouve en ce point x₁ de S₁ marque la date t₁ .

                                                                                page 5

Si l'extrémité B de AB passe en x'₁ de S₁ lorsque l'horloge de S₁ qui se trouve en ce point x'₁ de S₁ marque la même date t₁ , alors par définition, la mesure algébrique de segment AB est :
                                              x'₁ - x₁
 Ce nombre représente la différence d'abscisses des points de S₁ d'où l'on voit simultanément
par rapport à S₁ les extrémités du segment AB .

Cette définition est valable dans tout système de référence.
 
Exemple : Soit le segment AB immobile par rapport à S .

A d'abscisse 0 dans S , B d'abscisse 4 dans S ( voir figure 1).
Sur le premier dessin de la figure 1, l'origine A de AB se trouve au point d'abscisse x₁ = 0 de S₁ ,
et l'horloge de S₁ qui se trouve en ce point marque la date t₁ = 0 .

Sur le second dessin de la figure 1 , l'extrémité B de AB se trouve au point d'abscisse
x'₁ = 2 de S₁ , et l'horloge de S₁ qui se trouve en ce point marque également la date 0 .
 
Donc dans S₁ , à " l'instant " t₁ = 0 (de S₁ ) , l'origine A de AB est vue en x₁ = 0 , et l'extrémité
B est vue en x'₁ = 2 . La mesure algébrique de AB par rapport à S₁ est donc :
 
x'₁ - x₁ = 2 - 0 = 2 .

Le segment AB a donc pour longueur 2 dans S₁ . Un segment de longueur 4 de S est vu sous la longueur 2 dans S₁ .

Nous voyons immédiatement grâce à nos dessins de la figure 1 , qu'un segment de longueur 4 , pris
sur S₁ (et mesuré dans S₁ ), a pour longueur 2 dans S .

                                                                                page 6

Systèmes mécaniques obéissants aux transformations de Lorentz.

1° Système construit (d'apparence arbitraire) .

Soit un axe Ox immobile dans un espace-temps classique. L'axe est noté S .

Soit un axe O₁x₁ noté S₁ , parallèle à Ox et se déplaçant à la vitesse v = 3 par rapport à Ox ( de façon classique ).

De manière axiomatique nous prenons l'unité de longueur sur S₁ égale à la moitié de celle de S , et en chaque point de S₁ nous plaçons une horloge , horloges qui marchent toutes à une vitesse deux fois plus lente que celles de S , et qui sont déphasées les unes par rapport aux autres , déphasage qui vaut -1/4 pour une différence d'abscisse de 1 sur S₁ . De plus , l'horloge qui se trouve en O₁ , origine de S₁ marque 0 à la date t = 0 de S .
 
Plus rapidement , nous mesurons sur S₁ les distances et les temps comme cela est indiqué sur les dessins de la figure 1.
 
La manière de mesurer les temps dans S₁ n'a rien de choquante , il suffit de penser aux fuseaux horaires terrestres.
Les événements qui se déroulent à Paris sont datés par les horloges parisiennes , tandis que ceux qui se déroulent à New York sont datés par les horloges de cette ville . Lorsque l'on dit qu'une explosion s'est produite à New York à midi , il est toujours sous-entendu que l'heure est donnée par l'horloge de cette ville. De même pour toute autre ville.
 
Revenons à nos systèmes. Soit E un événement (explosion par exemple) qui se produit au point d'abscisse x de S , à la date t de S .
t est donné par l'horloge de S qui se trouve au point d'abscisse x de S , mais cela n'a pas d'importance, car S est un système classique dont toutes les horloges sont synchrones .
 
L'abscisse x₁ mesurée dans S₁ de ce événement , ainsi que la date t₁ donnée par l'horloge de S₁ qui se trouve au centre de cet événement E ( horloge au point d'abscisse x₁ de S₁ ) lorsqu'il se produit , sont donnés par :
 

 

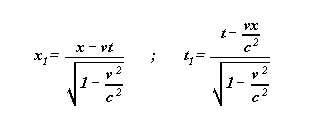
Avec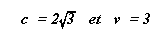
 
 On passe de S à S₁ par les transformations de Lorentz , ce que l'on peut expérimenter avec différents événements sur les dessins de la figure 1 ou de la figure 2 .
On remarque que connaissant x₁ et t₁ , on retrouve x et t a l'aide des deux formules précédentes en remplaçant v par -v , c'est à dire que :
 
                                                                                page 8

 
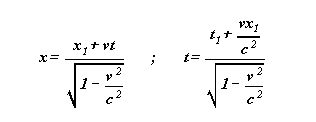
Nous passons de S₁ à S par les transformations de Lorentz de même constante c .
Nous avons donc deux systèmes matériellement construits et tels que l'on passe de l'un à l'autre par les transformations de Lorentz de même constante c .
 La symétrie de ces transformations n'implique nullement que les systèmes S et S₁ soient analogues du point de vue matériel. Dans nos dessins , les systèmes sont totalement dissemblables , et en les voyant, il ne viendrait à l'idée de personne de dire qu'ils sont équivalents, et pourtant , on passe de l'un à l'autre par les mêmes transformations.

Nous verrons plus loin que ces deux systèmes ne sont pas du tout équivalents pour la description de certains phénomènes , en particulier les mobiles qui se déplacent dans S à des vitesses plus grandes que c , conduisent à certains ( pseudo ) paradoxes dans S₁ , paradoxes tout à fait équivalents à ceux obtenus sur la terre rapportée à ses fuseaux horaires. Un avion très rapide qui part de Paris à midi (heure parisienne) peut arriver à onze heures à New York ( heure de New York ) , et jamais personne ne s'en offusque comme on le ferait en relativité.
 

2° Système mécanique naturel en mécanique classique..
 On peut se poser la question de savoir s'il existe en mécanique classique des systèmes qui naturellement obéissent aux transformations de Lorentz , c étant une constante attachée aux systèmes.

La réponse est oui , et il est même étonnant de voir qu'ils sont très courants.
 
Considérons une corde élastique (parfaite) Ox , rapportée au repère orthonormé Oxy . Toute onde
transversale (de direction Oy ) sur la corde est définie par deux fonctions (quelconques) f et g .
 
A toute date t , le point d'abscisse x de la corde a pour ordonnée y = f(ct -x) + g(ct + x)
 
c étant une constante positive attachée aux caractéristiques mécaniques de la corde. c est tout simplement la vitesse des ondes (transversales) sur cette corde vibrante.
 
y = f(ct -x) est une onde se propageant de gauche à droite à la vitesse c , y = g(ct + x) est une onde se

propageant de droite à gauche à la même vitesse sur cette même corde. La somme de ces deux ondes donne l'état de la corde vibrante à toute date t , c'est l'onde résultante.
 
Soient t' et x' les transformées de x et t par les transformations de Lorentz.
 
 
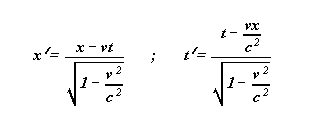
 Comme auparavant posons :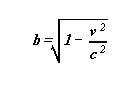

                                                                                page 9

Calculons ct' - x' ainsi que ct' + x'
 Nous trouvons que :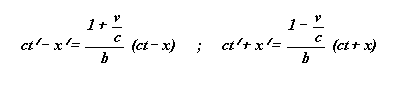
 Posons :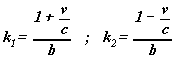  
   k₁ et k₂ sont deux constantes qui ne dépendent ni de x ni de t .
 Nous avons ainsi :

   ct' - x' = k₁ ( ct - x ) et que ct' + x' = k₂ ( ct + x )

 y = f(ct' -x') + g(ct' + x') = f(k₁ (ct -x)) + g(k₂ (ct + x))

y = f(ct' -x') - f(ct' + x') = f(k₁ (ct -x)) - f(k₂ (ct + x)) , le point d'abscisse x = vt a toujours pour ordonnée y = 0 , ce qui est facile à vérifier.

Les points "fixes" de la perturbation au " repos" , sont convertis en points "fixes" à vitesse v dans la perturbation en mouvement.
 
Les questions que l'on se pose maintenant sont :
Que sont nos horloges sur la corde ?
Et que deviennent-elles lorsque la perturbation est mise à vitesse v ? .

Les mêmes questions se posent pour les unités.
 
Voici la réponse:
En chaque point de la corde , pour un système immobile , les temps sont tout simplement donnés par une perturbation périodique stationnaire de référence .L'unité de temps étant proportionnelle à la période vibratoire.

L' unité de longueur est définie par cette même perturbation de référence , l'unité prise étant proportionnelle à la distance de deux points fixes consécutifs .

Dans tout système mis à vitesse v le long de Ox , les références de temps et de longueurs sont données par la perturbation de référence mise à vitesse v le long de Ox , selon les transformations de Lorentz , comme cela est indiqué ci-dessus.

Précisons ceci sur un exemple, c'est l'exemple affiché lorsque l'on démarre le programme joint.
 
                                                                                page 10

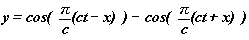
L'unité de mesure est la distance entre deux points immobiles consécutifs divisée par c .

En chaque point du système immobile se trouve une horloge , horloge qui augmente d'une unité chaque fois que l'onde traverse l'axe Ox sous ses pieds.
La période vibratoire de cette onde est : T = 2 . L'axe Ox est traversé par la corde toute les unité de temps.
 
Si nous mettons le système en mouvement à vitesse v le long de l'axe Ox , les temps et les distances
dans le système en mouvement sont donnés par l'onde de référence mise à vitesse v, soit par l'onde :

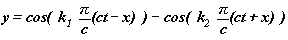
Les points "immobiles" se déplacent selon Ox à la vitesse v .

Les points "immobiles" sont les points d'abscisses x = vt +bkc , k constante entière positive ou négative, b étant défini plus haut.
On voit que les points fixes se sont rapprochés selon le facteur multiplicatif b .

Une observation attentive de l'animation du programme joint permet de comprendre parfaitement les explications ci-dessus.
 
Cette façon naturelle de mesurer temps et distances à l'aide d'une onde de référence , explique totalement les transformations de Lorentz sans sortir du cadre de la mécanique classique.
 
Complément : Si Eo représente l'énergie totale de l'onde au repos entre deux points fixes,
énergie qui prend en compte l'énergie potentielle des forces exercées par l'onde sur les extrémités du système,
nous trouvons que l'énergie totale Ev du système mis à vitesse v est Ev = Eo/b

La démonstration sort du cadre de cette étude élémentaire.

Le système se comporte vis à vis de l'accélération comme une masse m = Ev / c^{2 .}
 

Les résultats obtenus sur une corde vibrante sont généralisés aux milieux élastiques de dimension trois.
 
 
 
Etude expérimentale de mobiles qui se déplacent à vitesses plus grandes que c dans S
 

Cette petite étude n'a pour but que de souligner certains paradoxes qui prouvent que les systèmes
S et S₁ ne sont pas équivalents . S permet de décrire de façon cohérente le mouvement d'un mobile
qui se déplace à une vitesse plus grande que c , la description de ce même mouvement dans S₁ devient
paradoxale (ou incohérente).

                                                                                page 11

Avec toujours :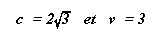
 Soit M un mobile qui se déplace à la vitesse v = 3.5 par rapport à S , son équation horaire dans S étant x = 3.5 t

A t = 0 de S , M est en x = 0 de S , il est perçu dans S₁ au point d'abscisse x₁ = 0 , et l'horloge de S₁ qui se trouve en ce point marque la date t₁ = 0.
A date t' = 2 de S , M se trouve en x' = 7 .
Il est alors perçudans S₁ au point d'abscisse x'₁ = 2 , et l'horloge de S₁ qui se trouve en ce point marque la date t'₁ = 1/2 .
La vitesse de M mesurée par rapport à S₁ est (x'₁- x₁)/(t'₁ - t₁) = 2/0.5 = 4 .
La mesure de la vitesse de M par rapport à S₁ donne une valeur plus grande que celle obtenue dans S , vitesses toutes deux plus grandes que c .
Ce résultat semble contraire au bon sens qui suggère pour vitesse de M dans S₁ une valeur inférieure à celle obtenue dans S puisque M et S₁ de déplacent dans le même sens.

Ce paradoxe est simplement du à la manière dont on mesure temps et distances dans S₁
 
 Soit maintenant N un autre mobile qui se déplace dans S à la vitesse 4 .
Dans S₁ , les horloges qui coïncident avec N marquent toujours 0 .
Le mobile N passe devant chaque horloge de S₁ lorsque cette dernière marque 0 . ( voir la figure 3)
N est donc selon S₁ partout à la fois à la date 0 , la vitesse de N par rapport à S₁ est infinie .
S₁ est donc un système de référence dans lequel il est impossible de décrire le mouvement de N .
De ce point devue , S et S₁ ne peuvent pas être équivalents.
 
 Considérons cette fois le mobile P de vitesse v = 5 par rapport à S .
L'équation du mouvement de P dans S est prise égale à x = 5 t .
Le mobile passe en O, origine de S, à la date t = 0 de S.
Les coordonnées de P dans S₁ sont alors x₁ = 0 et t₁ = 0 .
A t' = 1 de S ce même mobile P se trouve au point d'abscisse x' = 5.
Comme auparavant, en s'aidant de la figure 3, on trouve que les coordonnées de P dans S₁ sont alors x'₁ = 4 et t'₁ = -1/2 .
 
Dans S₁ , nous avons donc : heure de départ de P en O₁, 0 h .
Heure d'arrivée de P en x'₁ = 4 , -1/2 h .
 
Dans S₁ , le mobile arrive 1/2 h avant qu'il ne soit parti.

Présentons ceci autrement; dans S₁ , un tireur tire une balle de O₁ à la date t₁ = 0 , et à la vitesse v = 5 par rapport à S .
Cette balle arrive en x'₁ = 4 de S₁ à la date t'₁ = -1/2 h de S₁ .
La balle, selon les mesures de S₁ arrive 1/2 h avant qu'elle ne soit partie.
Dans S₁ , pour certains phénomènes , l'effet précède la cause , ou plutôt semble précéder la cause.

Ce paradoxe est analogue à ceux créés par le décalage des fuseaux horaires terrestre.
 
Encore une fois , S₁ est inapte à une description cohérente de certains phénomènes. S et S₁ ne sont pas équivalents.
 
Ce fait permet d'ailleurs de déterminer qui de S ou de S₁ est immobile.
Le système immobile est celui dans lequel n'existe aucun paradoxe, c'est celui dans lequel l'effet ne précède jamais la cause.
 

Il est toujours possible de doubler S₁ d'un système S'₁ galiléen qui suit S₁ ( les horloges et les unités de S'₁ sont celles de la mécanique classique , celles de S ) . Dans S'₁ , les paradoxes disparaissent.

L'existence simultanée de différents types de systèmes de référence n'est nullement contradictoire .
Un système de Lorentz ( relativiste) , peut toujours être doublé par un système galiléen, système dans lequel il est plus facile de raisonner .

                                                                                page 13

Soit un système S₂ qui coïncide avec S₁ . S₂ quitte S₁ , puis rejoint S₁ en faisant coïncider les unités.
On s'aperçoit alors que les horloges de S₂ sont en retard par rapport à celles de S₁ , et ceci quelques soient les accélérations intermédiaires de S_{2 ,} S₁ poursuivant son mouvement uniforme. Sur le programme joint , le bouton T permet de faire cette expérience. On peut bien sûr faire différents dessins comme ceux des figures 1,2,3 avec trois systèmes pour visualiser ce paradoxe. Ce paradoxe s'explique uniquement par les formules de Lorentz, sans intervention d'aucune autre théorie.
 

Cabala Serge . 1975 , 1976, 1977 , 1980 , .... , 14 juin 1999 , 2 février 2002
 

P.S.
 

Mes principaux travaux sur ce sujet:

Cette étude.
La relativité par les cordes vibrantes. (1975-76) classé aux archives originale du CNRS depuis 1977 (183 pages).
La relativité par les milieux élastiques (1981 , 185 pages)
Changements de variables transformant toute fonction de d'alembertien nul en une fonction de d'alembertien nul , avec extension aux équations de Klein-Gordon (1988 , 129 pages)
 
Tous ces travaux sont reconnus , un ancien directeur du CNRS en souligne la bonne qualité.
Ils ne sont pas enseignés ni publiés à grande échelle de manière à ne pas déranger la relativité traditionnelle.

Il est regrettable que la science se soit transformée en religion , en maintenant certains dogmes inutiles et contraignants, tel le principe de relativité accompagné de sa vitesse limite .

Les formules de relativité n'étant que des formules de mécanique classique de milieux élastiques, il est donc inutile de vouloir les établir à partir de principes nouveaux, principes qui de plus limitent arbitrairement leurs applications, et introduisent une note peu cartésienne .
 
 Quand on parle de relativité , on cite toujours les expériences de Michelson et Morley , faites en 1881 et 1887 , sur la détection du vent d'éther par rapport à la terre.

Que l'on réfléchisse un peu , après avoir lu ce qui précède et utilisé le programme sur les ondes.

Si les champs électromagnétiques ne sont que des "ondes" particulières de l'éther considéré comme un milieu élastique, la seule façon de mettre ces "ondes" ou champs électromagnétiques en translation uniforme, c'est d'utiliser les transformations de Lorentz .

Les atomes de matière sont liés les uns aux autres par des champs électromagnétiques "stationnaires"

La mise en translation uniforme d'une règle matérielle quelconque dans le sens de sa longueur met les "ondes stationnaires" en mouvement , ces ondes se contractent dans le sens du mouvement et se déphasent (voir le programme) , les atomes de la règle se rapprochent et la règle raccourcit .

Le vent d'éther devient ainsi indétectable par cette expérience.

L'explication du résultat négatif de l'expérience, par la contraction des corps en mouvement, avait déjà été donnée en son temps par Fitzgerald (1893), mais la constitution atomique actuelle de la matière n'étant pas connue (l'atomisme était même fortement combattu par des savants célèbres), cette explication mécanique semblait difficilement admissible . On ne pouvait concevoir que des matériaux de duretés très différentes puissent se contracter de la même façon.

L'expérience de Michelson et Morley , finement analysée est en faveur de l'éther.

                                                                                    page 14

Il en est de même de l'expérience de Michelson et Morley , grossièrement analysée , elle est en défaveur de l'éther, finement analysée, elle en devient une des preuves.
 
 

J'espère vous avoir communiqué le plaisir d'une relativité enfin cartésienne.

Serge CABALA

                                                                                        page 15

.