RELATIVITE ET ONDES
Voir et comprendre la mécanique
des onde.
Auteur : Serge CABALA
Cliquer sur "Home
page" pour obtenir
la page principale
Ondes sur un plan, page
5/5
Interféromètre,
réseaux
A) Interféromètre.
Un interféromètre est un appareil qui permet
de produire et d'observer le résultat de superpositions d'ondes
(interférences d'ondes).
L'interféromètre de Michelson permet de
mesurer des différences de distances de l'ordre du quart de longueur
d'onde.
La source qui se trouve dans le bras gauche, envoit des
ondes sur une paroi (à peu près) demi-réféchissante.
Une partie des ondes poursuit son chemin dans le bras
droit, tandis qu'une autre est réfléchie dans le bras du
haut.
Les extrémités des bras droit et haut sont
fermés par des parois réféchissantes.
Les ondes renvoyées passent de nouveau par la
paroi demi réfléchissante, et une partie de chaque onde réfléchie
se retrouve dans le bras du bas.
En supposant que la paroi demi-réfléchissante
ne déphase pas l'onde tansmise par rapport à celle réfléchie,
pour des bras (le droit et le haut) de même
longueur, ou qui ne diffèrent que d'un mutiple entier de la demi-longueur
d'onde employée, on voit une onde sortir par le bas.
Si les bras diffèrent d'un quart de longueur d'onde,
ou d'un multiple impair du quart de longueur d'onde, le résultat
dans le bras du bas est nulle ou très atténué.
L'annulation de l'onde dans le bras du bas n'est jamais
parfaite.
Remarque: l'appareil est encore utilisable lorsque la
paroi demi-réfléchissante déphase les ondes transmises
et réfléchies, ou modifie leurs intensités relatives.
Interféromètre de Michelson
I
Ici la paroi demi-réfléchissante
ne déphase pas l'onde réfléchie par rapport à
celle qui traverse.
Bras égaux.
 L'onde sortante est à son maximum.
L'onde sortante est à son maximum.
|
Bras droit raccourci.
 L'onde sortante est à son minimum.
L'onde sortante est à son minimum.
|
Sur la figure de droite, le bras doit est diminué
du quart de la longueur d'onde de la source.
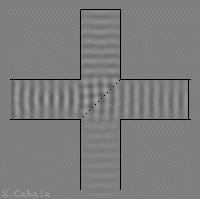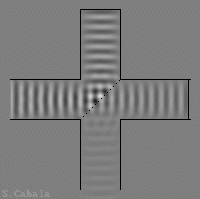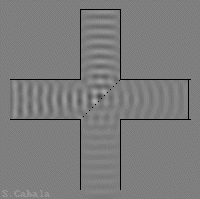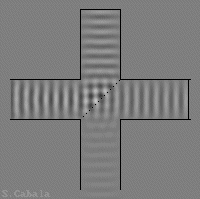
Interféromètre de Michelson
II
Dans ces animations, la paroi demi-réfléchissante
déphase les ondes transmises et réfléchies.
Bras égaux.
 L'onde sortante est maximale.
L'onde sortante est maximale.
|
Bras droit raccourci.
 L'onde sortante est minimale.
L'onde sortante est minimale.
|
Sur l'animation de droite, la paroi réfléchissante,
est déplacée du quart de la longueur d'onde de la source.
B) Réseaux.
Le fonctionnement d'un réseau est assez difficile à
saisir, j'espère que les animations suivantes aiderons à
comprendre.
En optique, les réseaux sont des
lames transparentes ou réfléchissantes qui comportent un
très grand nombre de stries parallèles équidistantes.
La distance entre deux stries est
appelée pas du réseau. Un bon réseau comporte environ
600 stries par millimètre, ce qui donne un pas de 1,66 millième
de mm.
La lumière visible ayant une
longueur d'onde comprise entre 0,4 et 0,75 millième de mm, on constate
que le pas d'un bon réseau est à peine deux fois plus grand
que la plus grande longueur d'onde visible (couleur rouge).
Des réseaux ayant seulement
40 stries par millimètre sont déjà utilisables en
lumière visible, tandis que ceux au pas trop fin ne le sont plus.
Prenons un réseau sur une lame
transparente. En regardant une lumière blanche à travers,
on voit, en pivotant cette lame, apparaître les couleurs du spectre
lumineux.
Tout comme un prisme, le réseau,
ou réseau de diffraction, dévie chaque rayon lumineux d'un
angle qui dépend, entre autre, de sa longueur d'onde.
Les avantages par rapport au
prisme sont:
- Une meilleure
séparation des couleurs.
- Connaissant
le nombre de stries au millimètre, l'angle d'incidence et l'angle
de déviation, on peut calculer la longueur d'onde d'un onde monochromatique
incidente.
Les disques DVD, bien qu'ayant des stries circulaires,
forment de bons réseaux par réflexions, lorsqu'on se limite
à des des secteurs étroits.
En optique, les réseaux se divisent en deux types :
> Les réseaux par transmission, qui sont
gravés sur des lames transparentes, où l'on examine la lumière
qui les traverse.
> Les réseaux par réflexion, qui sont
gravés sur des miroirs, où l'on étudie la lumière
qu'ils renvoient.
De plus, il y a différentes façons d'utiliser un réseau.
a) On éclaire le réseau à l'aide
d'une source en forme de fente, parallèle aux stries du réseau,
qui donne un fin pinceau rectangulaire perpendiculaire au plan du réseau.
Ici, seule une petite partie du réseau est utilisée. Cette
méthode est souvent employée, car très commode, et
spectaculaire en lumière blanche, elle donne de beaux étalements
du spectre..
b) On éclaire le réseau avec une lumière
plus ou moine rasante (le soleil qui éclaire obliquement le réseau
par exemple).
Les animations qui suivent illustrent ces deux utilisations.
Le résultat obtenu par un réseau est expliqué (en
gros) par le principe de Huygens. De chaque strie, sort une onde circulaire
(cylindrique) qui interfère (s'ajoute algébriquement) aux
ondes circulaires qui sortent des autres trous.
Utilisation a)
Source plane orthogonale.
Réseau par transmission.
En optique, la source est une fente lumineuse au-dessus et
parallèle au réseau, ce qui correspond aux sources ci-dessous.
Dans ce cas, les résultats sont symétriques.
Source plane réduite, orthogonale
au réseau.
Fréquence (F) élevée.
 Dispersion moyenne
Dispersion moyenne
|
Fréquence (f) faible.
 Plus forte dispersion
Plus forte dispersion
|
Mélange de (F) et (f)
 Sépartion des fréquences.
Sépartion des fréquences.
|
On remarque trois branches
principales sur les deux premières images.
Ces branches s'écartent
d'autant plus que la longueur d'onde est grande (la fréquence est
faible).
Sur l'animation de droite,
les différentes fréquences de la source se séparent
à la sortie du réseau,
les grandes longueurs d'ondes
étant les plus extérieures.
Image en couleur.
Plusieurs fréquences colorées en entrée.
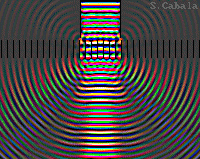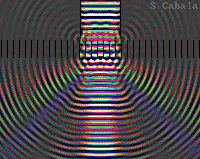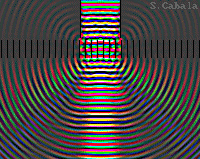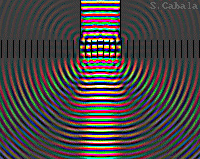 Séparation des couleurs par le réseau.
Séparation des couleurs par le réseau.
|
Remarque: sur un long réseau,
lorsque la fin de la source rectangulaire est plus haute, les
ondes qui sortent de ses bords ,deviennent rasantes, et peuvent,
suivant les résultats de l'utilisation b), donner de nouvelles
images de diffraction, affaiblies, et même inversées
pour l'ordre des fréquences.
Utilisation b)
Source plane oblique.
I
Réseau par transmission.
L'onde plane arrive obliquement
par la gauche au dessus du résau avec un angle plus ou moins grand.
Les lignes du réseau
se comportent comme un rasoir à lames multiples.
Chaque morceau d'onde coupé
passe par l'espace entre deux stries et forme à la sortie une onde
en rond en vertu du principe de huygens.
Comme l'espace entre les stries
est légérement différent de la longueur d'onde qui
s'étale en biais, les pulsations entre les stries sont déphasées.
Les ondes en rond qui en sortent
sont toutes égales mais déphasées.
L'assemblage de toutes ces
ondes sortantes donne entre autres, l'onde plane descendante granulée
que l'on voit.
Ces lignes granulées proches de l'horizontale
sont des lignes d'égale intensité (au granulations près)
.
Ci-dessous, sur le même réseau,
trois animations avec des longueurs d'ondes différentes.
Dans ces images, la longueur
d'onde qui s'étale en bias sur le réseau est légérement
plus grande que son pas, ce qui explique la pente vers la droite.
Longueur d'onde la plus petite. (1)

|
Longueur d'onde intermédiaire.
(2)

|
Longueur d'onde la plus grande. (3)

|
On remarque ici, que la grande longueur d'onde,
donnent les lignes les plus penchées à droite.
Une partie de l'onde plane incidente est réfléchie
par le réseau et s'y superpose,
ce qui donne les escaliers que l'on voit au dessus
du réseau.
Pour mieux voir que ces lignes
granuleuses obliques, donnent des ondes planes qui avancent suivant la
direction qui leur est perpendiculaire, on met un collimateur sous le réseau,
ici une simple surface absorbante percée d'un trou.
La pupille d'un oeil est un collimateur.
Le collimateur sous le réseau
permet de voir que les lignes granuleuses sont des ondes .
Longueur d'onde la plus petite. (1)

|
Longueur d'onde intermédiaire.
(2)

|
Longueur d'onde la plus grande. (3)

|
Le collimateur donne en sortie une onde principale
très visible,
dont la direction de propagation, est perpendiculaire
aux lignes granuleuses.
(Sous le collimateur, de chaque coté du flux
principal, on voit d'autres interférences.)
On peut se demander si l'orientation
et la dimension du trou du collimateur influence la direction de sortie.
L'orientation du collimateur sous
le réseau ne modifie pas la direction du flux principal qui en sort.
Ici, seule la position du collimateur
change.
La longueur d'onde est un peu
supérieure à celle des images précédentes,
ce qui donne une plus grande
déviation.
La meilleure orientation du collimateur est
celle de droite.
Collimateur à large ouverture.
Le flux pincipal garde toujours
la même direction.
II
Réseau par réflexion.
En optique, dans un réseau par transmission,
la lumière traverse une lame transparente.
Or cette lame atténue ou bloque certaines
longueurs d'ondes (le verre atténue ou bloque les infra-rouges et
les ultra-violets),
d'où l'utilisation de réseaux par réflexion
qui ne bloquent théoriquement rien.
Un miroir sous le réseau renvoie
les diffractions vers le haut.
Correspond à l'image (2) plus haut.
 Sans collimateur.
Sans collimateur.
|
 Avec collimateur.
Avec collimateur.
|
Ici la source plane est réduite pour
mieux voir les ondes diffractées.
Le collimateur permet de mieux discerner les rayons
diffractés
Remarque: la distance inter-stries d'un
réseau peut être de plusieurs fois la longueur d'onde, dans
ce cas, l'angle d'incidence de l'onde plane devra être plus vertical
pour avoir un plus grand étalement de l'onde sur ce réseau.
Le résultat est beaucoup plus granuleux.
Ondes planes de même fréquence
sur deux réseaux de densité différente.
L' incidence sur le gros réseau
est adaptée pour avoir une sortie parallèle au réseau
fin.
Réseau fin, onde incidente rasante.
 Granulations fines.
Granulations fines.
|
Gros réseau, incidence plus verticale.
 Grosses granulations.
Grosses granulations.
|
Réseau fin , et collimateur.
 Sortie sombre.
Sortie sombre.
|
Gros réseau, et collimateur.
 Sortie plus claire.
Sortie plus claire.
|
Pour le gros réseau, le trou du collimateur
est plus important pour laisser passer plusieurs granulations.
Autre remarque: en optique, les ondes qui sortent d'un
réseau grossier, donnent l'impression d'être vues à
travers un brouillard, cela se traduit par les granulations que l'on voit
sur les animations ci-dessus.
Jusqu'ici, la longueur d'onde qui s'étale
en biais sur le réseau dépasse légérement le
pas de ce réseau.
Qu'obtient-on lorsqu'elle est légérement
inférieur au pas?
La réponse est donnée par cette image.
La ligne granulée semble pencher vers la gauche,
mais c'est perpendiculairement à la ligne
granulée très verticale qui penche vers la droite,
que l'on trouve le flux principal en sortie de collimateur,
flux gauche sur l'image.
C) Miroirs de Fresnel.
Au début du XIX ième siècle, la théorie corpusculaire
de la lumière était la théorie officielle.
Agustin Fresnel (1788-1827) partisant de la théorie ondulatoire,
décrivit en juillet 1816, une dispositif original soutenant son
point de vue.
Les excellents résultats obtenus finirent, avec l'aide
d'Arago, par convaincre les membres de l'Académie que la lumière
était bien de nature ondulatoire.
Beaucoup pensaient depuis au moins deux siècles, au vu d'un
grand nombre d'observations, que la lumière était une onde
(Descartes Grimaldi, Huygens, Euler, Young ), mais jusqu'à Fresnel,
rien ne semblait atteindre ses opposants (les partisans de la théorie
corpusculaire).
Les miroirs de Fresnel ont une grande importance historique, mais ne
représentent qu'un dispositif de plus en faveur des ondulations
lumineuses.
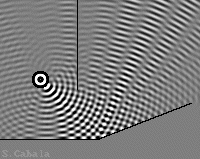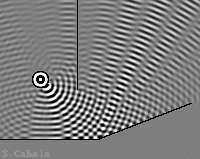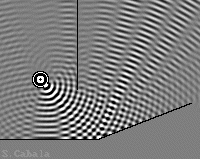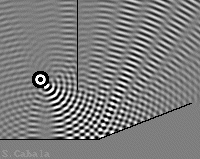
L'image centrale représente le
dispositif de Fresnel.
Il est formé de deux miroirs plans
faisant entre eux un angle obtu.
Ici, l'un est horizontal, l'autre oblique.
Un source collimatée, envoit ses
rayons en direction du sommet de l'angle.
Une paroi verticale absorbante ne laisse
passer à droite que les rayons en provenance des miroirs.
On obtient de larges interférences
sur la partie droite de l'image centrale.
Miroir droit enlevé.
 Interférences nulles ou serrées.
Interférences nulles ou serrées.
|
Dispostion de Fresnel.
 Larges interférences à droite.
Larges interférences à droite.
|
Miroir gauche enlevé.
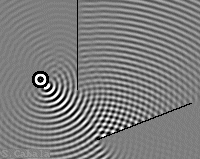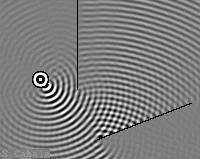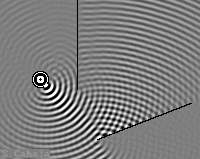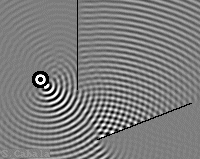 Interférences nulles ou serrées.
Interférences nulles ou serrées.
|
En optique, du fait de la très petite longueur
d'onde de la lumière,
l'angle des miroirs est plus obtu, et la source lumineuse
plus rasante.
Le calcul permet de positionner le système.
Ondes sur un plan.
Accès direct aux pages.
|
Page 1
Réflexions.
|
Page 2
Réflexions.
|
Page 3
Huygens, Young.
|
Page 4
Dioptres, prismes, lentilles.
|
Page 5
Intèrféromètre, réseaux,
miroirs de Fresnel.
|





























